TP 2 : Simulation de variables aléatoires
Contents
TP 2 : Simulation de variables aléatoires#
Dans ce TP, nous allons simuler des lois de variables aléatoires à partir d’une variable uniforme sur \([0, 1]\).
Modules à importer :
from collections import Counter
import matplotlib.pyplot as plt
import random
import numpy as np
La fonction suivante permettra de comparer l’histogramme obtenu avec la loi correspondante dans numpy, pour vérifier votre code :
def test_hist(n, var, var_validation, *args):
fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(15, 5))
for i, f in enumerate([var, var_validation]):
d = Counter([f(*args) for _ in range(n)])
s = sum(d.values())
axes[i].bar(d.keys(), [v/s for v in d.values()])
axes[i].set_xlabel(f"valeur de X = {f.__name__}(p)")
axes[i].set_ylabel("fréquence d'apparition de X")
axes[i].set_title(f"Histogramme de {'np.random.' if i == 1 else ''}{f.__name__}(p)")
plt.show()
Loi de Bernoulli#
On rappelle que \(X\) suit une loi de Bernoulli de paramètre \(p\) si :
On utilisera la fonction random.random qui génère un flottant aléatoire entre \(0\) et \(1\) (c’est-à-dire une variable aléatoire uniforme \(\mathcal{U}\) sur \([0, 1]\)) :
random.random()
0.8432888054435626
Exercice
En utilisant random.random(), écrire une fonction flip() simulant une loi de Bernoulli de paramètre \(p = 0.5\) (flip() doit renvoyer \(0\) ou \(1\), avec probabilité \(0.5\)).
Solution
def flip():
if random.random() > 0.5:
return 1
return 0
Exercice
Écrire une fonction bernoulli(p) simulant une loi de Bernoulli de paramètre p. On pourra adapter la fonction précédente.
Solution
def bernoulli(p):
if random.random() < p:
return 1
return 0
Exercice
Écrire une fonction test_bernoulli(p, n) telle que test_bernoulli(p, n) génère \(n\) fois une loi de Bernoulli de paramètre \(p\) et renvoie une liste L telle que L[0] est le nombre de \(0\) obtenus et L[1] est le nombre de \(1\).
Vérifier que vous obtenez autant de \(0\) que de \(1\) si \(p = 0.5\), et deux fois plus de \(0\) que de \(1\) si \(p = \frac{1}{3}\).
Solution
def test_bernoulli(p, n):
L = [0, 0]
for k in range(n):
L[bernoulli(p)] += 1
return L
print(test_bernoulli(0.5, 1000))
print(test_bernoulli(0.33, 1000))
Loi géométrique#
On rappelle que \(X\) suit une loi géométrique de paramètre \(p\) si :
Remarque : une loi géométrique correspond au nombre de fois qu’il faut générer une loi de Bernoulli de paramètre \(p\) avant d’obtenir \(1\).
Exercice
En utilisant la remarque précédente, écrire une fonction geometrique(p) simulant une loi géométrique de paramètre p.
Solution
def geometrique(p):
n = 0 # nombre de loi de Bernoulli qu'il a fallu générer
while bernoulli(p) == 0: # tant que la loi de Bernoulli donne 0
n += 1 # augmenter n de 1
return n + 1
Exercice
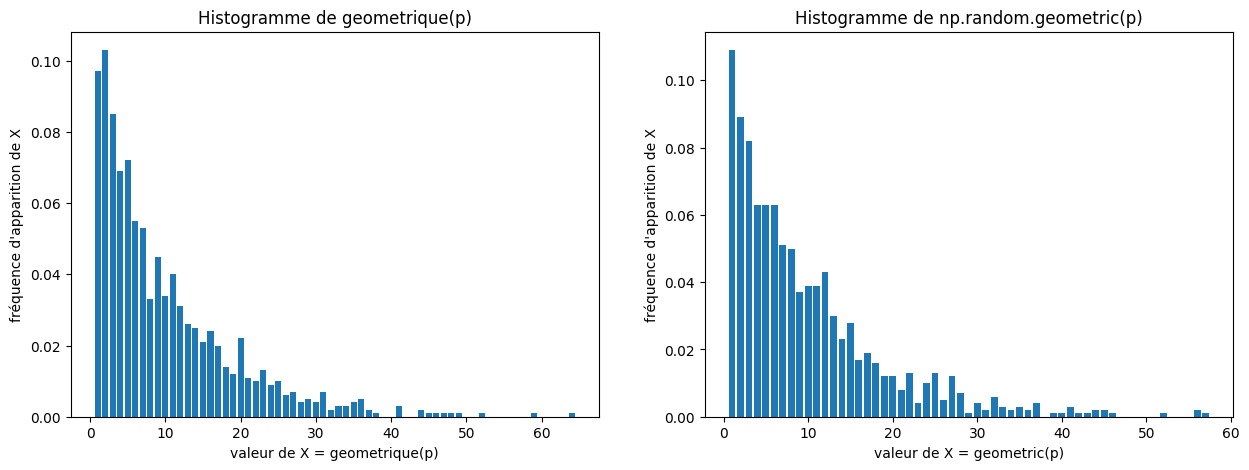
Tester en appelant la fonction test_geometrique(p, n) ci-dessous (on pourra prendre \(n = 1000\) et \(p = 0.5\), par exemple), qui appelle n fois votre fonction geometrique(p) et dessine l’histogramme obtenu. Un histogramme obtenu avec la fonction np.random.geometric est aussi affichée à droite (les deux dessins doivent se ressembler fortement, comme sur l’exemple ci-dessous).
def test_geometrique(p, n):
test_hist(n, geometrique, np.random.geometric, p)
Loi binomiale#
\(X\) suit une loi binomiale de paramètres \(n\) et \(p\) si, pour \(k = 0, 1, ..., n\) :
Définition équivalente : \(X\) est une somme de \(n\) variables de Bernoulli de paramètre \(p\).
Exercice
En utilisant cette deuxième définition, écrire une fonction binomial(n, p) simulant une loi binomiale de paramètre \(n\), \(p\).
Solution
def binomial(n, p):
X = 0
for k in range(n):
X += bernoulli(p)
return X
Exercice
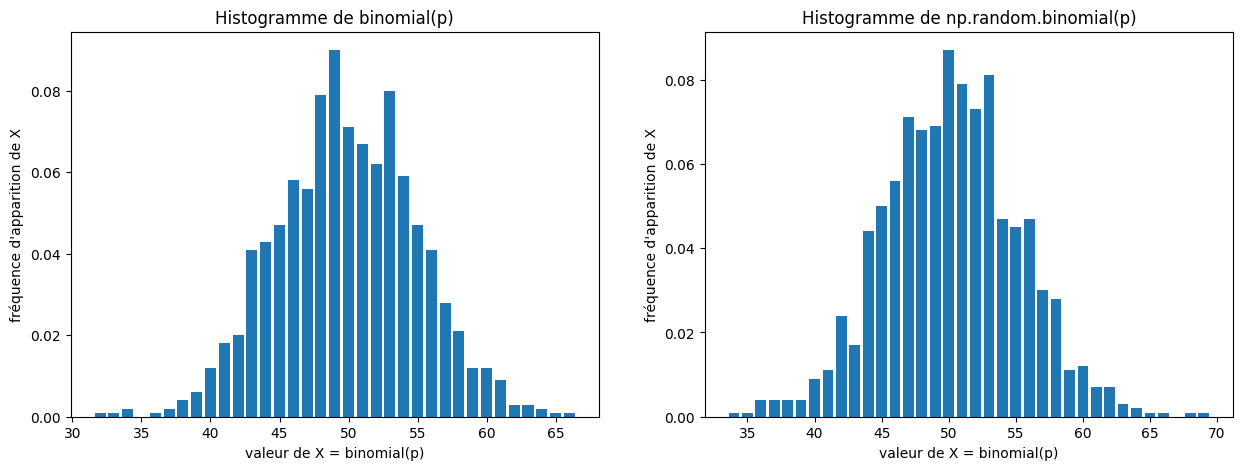
Tester avec la fonction suivante (prendre par exemple \(n = 100\) et \(p = 0.5\)). Vous devez obtenir un dessin ressemblant à celui ci-dessous.
def test_binomial(n, p):
test_hist(1000, binomial, np.random.binomial, n, p)
Simulation d’une loi normale à partir d’une loi Binomiale#
On rappelle que le théorème central limite :
Soient \(X_1\), …, \(X_n\) des variables indépendantes et de même loi, d’espérance \(\mu\) et d’écart-type \(\sigma\).
Soit \(S_n = X_1 + ... + X_n\). Alors \(\frac{S_n - n\mu}{\sigma\sqrt{n}}\) converge vers une loi normale centrée réduite.
Remarque : une loi normale est aussi appelée loi gaussienne.
Dans la suite, \(X_1\), …, \(X_n\) sont des variables de Bernoulli de paramètre \(p\) et \(S_n\) est une variable binomiale de paramètre \(n\), \(p\) (obtenue avec la fonction binomial ci-dessus).
Exercice
Calculer \(\mu\) et \(\sigma\) (sur papier, sans utiliser l’ordinateur).
Solution
Exercice
Écrire une fonction central_limite(n, p) renvoyant \(\frac{S_n - n\mu}{\sigma\sqrt{n}}\). On remplacera \(\sigma\) et \(\mu\) par les valeurs trouvées à la question précédente.
Solution
def central_limite(n, p):
return (binomial(n, p) - n*p)/(p*(1 - p)*n)**.5
Exercice
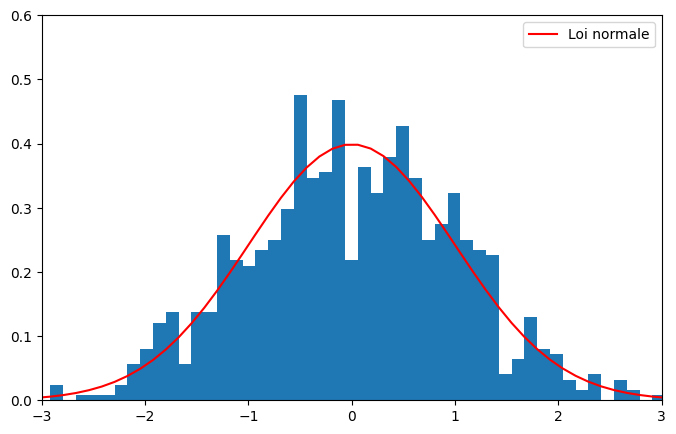
Tester avec la fonction ci-dessous, qui compare le résultat de \(\frac{S_n - n\mu}{\sigma\sqrt{n}}\) avec une loi normale centrée réduite. Vous devez obtenir un dessin similaire à celui ci-dessous.
def test_central(n, p):
mu, sigma = 0, 1
values = [central_limite(n, p) for _ in range(1000)]
plt.figure(figsize=(8, 5))
count, bins, ignored = plt.hist(values, 50, density=True)
plt.plot(bins, 1/(sigma*np.sqrt(2*np.pi))*np.exp(-(bins-mu)**2/(2*sigma**2)), color='r', label="Loi normale")
plt.axis([-3, 3, 0, .6])
plt.legend()
plt.show()
Méthode de la transformée inverse#
Définition : Soit \(X\) une variable aléatoire. Sa fonction de répartition \(F\) est définie par :
Théorème (admis) : Soit \(X\) une variable aléatoire de fonction de répartition \(F\) (supposée ici inversible) et \(\mathcal{U}\) une variable aléatoire uniforme sur \([0, 1]\). Alors \(F^{-1}(\mathcal{U})\) est une variable aléatoire de loi \(X\).
Remarque : Si \(F\) n’est pas inversible alors le théorème reste vrai en remplaçant \(F^{-1}\) par \(Q(u) = \inf\{x : F(x) \geq u\}\).
Comme nous savons comment simuler \(\mathcal{U}\) (avec random.random()), nous pouvons simuler n’importe quelle loi de probabilité, à condition de savoir inverser sa fonction de répartition.
Loi exponentielle#
Une variable aléatoire \(X\) est de loi exponentielle de paramètre \(a\) si sa fonction de répartition est, pour \(x\in \mathbb{R}^+\) :
Une loi exponentielle modélise la durée de vie d’un phénomène sans mémoire, ou sans vieillissement, ou sans usure : la probabilité que le phénomène dure au moins s + t heures (ou n’importe quelle autre unité de temps) sachant qu’il a déjà duré t heures sera la même que la probabilité de durer s heures à partir de sa mise en fonction initiale. En d’autres termes, le fait que le phénomène ait duré pendant t heures ne change rien à son espérance de vie à partir du temps t.
Exercice
Montrer que \(F^{-1}(y) = -\frac{\ln(1 - y)}{a}\) (sur papier, sans utiliser l’ordinateur).
Solution
D’où :
Exercice
En déduire une fonction exponentielle(a) simulant une loi exponentielle de paramètre a. On pourra utiliser np.log pour \(\ln\).
Solution
def exponentielle(a):
return -np.log(1 - random.random())/a
Exercice
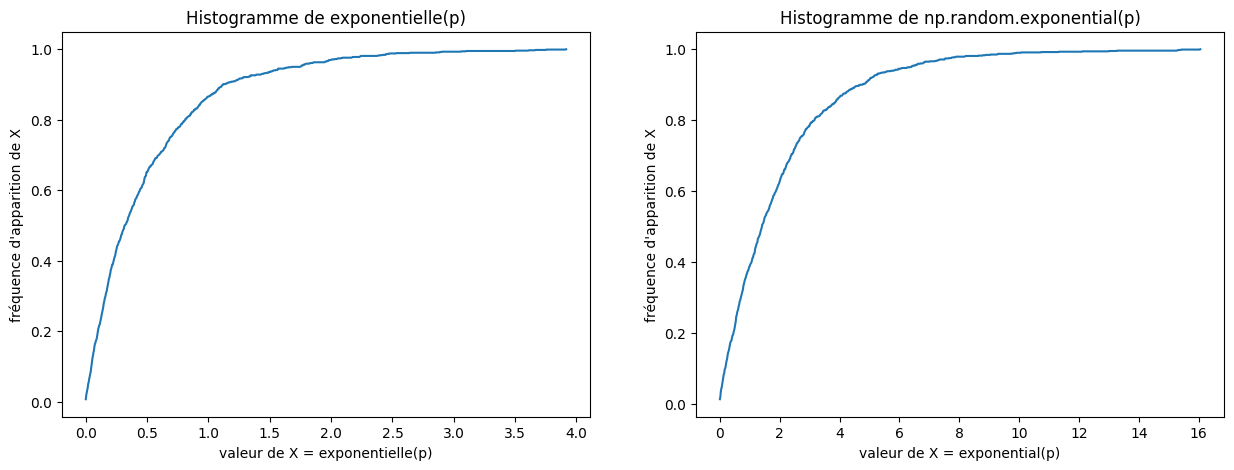
Tester avec la fonction suivante (prendre par exemple \(a = 2\) et \(n = 1000\)).
def test_exponentielle(n, a):
fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(15, 5))
for i, f in enumerate([exponentielle, np.random.exponential]):
if i == 1:
a /= 1
X = np.array([f(a) for _ in range(n)])
values, base = np.histogram(X, bins=1000)
axes[i].plot(base[:-1], np.cumsum(values)/sum(values))
axes[i].set_xlabel(f"valeur de X = {f.__name__}(p)")
axes[i].set_ylabel("fréquence d'apparition de X")
axes[i].set_title(f"Histogramme de {'np.random.' if i == 1 else ''}{f.__name__}(p)")
plt.show()
Loi de Poisson#
Une variable aléatoire discrète \(X\) suit une loi de Poisson de paramètre \(a\) si :
La loi de Poisson est une loi de probabilité discrète qui décrit le comportement du nombre d’événements se produisant dans un intervalle de temps fixé, si ces événements se produisent avec une fréquence moyenne ou espérance connue, et indépendamment du temps écoulé depuis l’événement précédent.
Simulation à partir de lois exponentielles#
On admet le théorème suivant permettant de simuler une loi de Poisson à partir d’une loi exponentielle :
Théorème : Soit \(X_1\), …, \(X_n\), … des variables exponentielles de paramètre \(a\). Soit \(S_n = X_1 + ... + X_n\). Soit \(Y\) la plus grande valeur de \(n\) pour laquelle \(S_{n} \leq 1\).
Alors \(Y\) suit une loi de Poisson de paramètre \(a\).
Exercice
Écrire une fonction poisson(a) simulant une loi de Poisson de paramètre a, en utilisant le théorème précédent. On pourra compléter le code suivant :
def poisson(a):
s = 0 # valeur de Sn
n = 0
while ...:
...
return n
Solution
def poisson(a):
s = 0 # valeur de Sn
n = 0
while s <= 1:
s += exponentielle(a)
n += 1
return n
Exercice
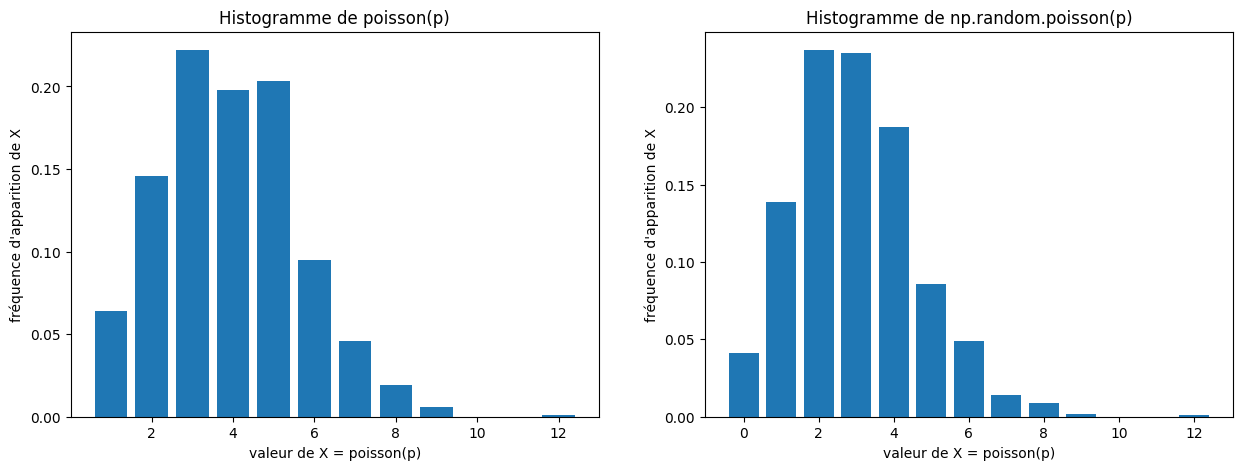
Tester avec la fonction suivante (prendre par exemple \(a = 3\) et \(n = 1000\)).
def test_poisson(a, n):
test_hist(n, poisson, np.random.poisson, a)
Approximation à partir d’une loi binomiale#
Exercice
(Difficile) Montrer (sur papier, sans ordinateur) que si \(np = a\) alors :
D’après l’exercice précédent, une loi binomiale de paramètres \(n\), \(p\) avec \(np = a\) converge vers une loi de Poisson de paramètre \(a\).
Exercice
En déduire une fonction poisson_approx(a) approximant une loi de Poisson en renvoyant une loi binomiale de paramètre \(n\), \(p\) avec \(np = a\). On prendra \(n\) assez grand, par exemple \(100\). Tester en comparant avec poisson(a).
Si vous avez terminé le TP, vous pouvez vous entraîner avec ces exercices.


