TP 11 : Basketball#

On souhaite lancer un ballon de basket depuis l’origine (le point de coordonnée $(0, 0)$) vers un panier de coordonnées $p$ généré aléatoirement :

import numpy as np
import matplotlib.pyplot as plt
plt.rcParams["figure.figsize"] = (12,6)
np.random.seed(0) # changer le 0 pour changer la position du panier

def panier():
    return np.random.randint(6, 10), np.random.randint(2, 5)
p = panier()
p # p[0] est l'abscisse du panier, p[1] est son ordonnée

(6, 3)

Trajectoire#

Étant donnée une vitesse initiale , on veut déterminer la trajectoire du ballon.

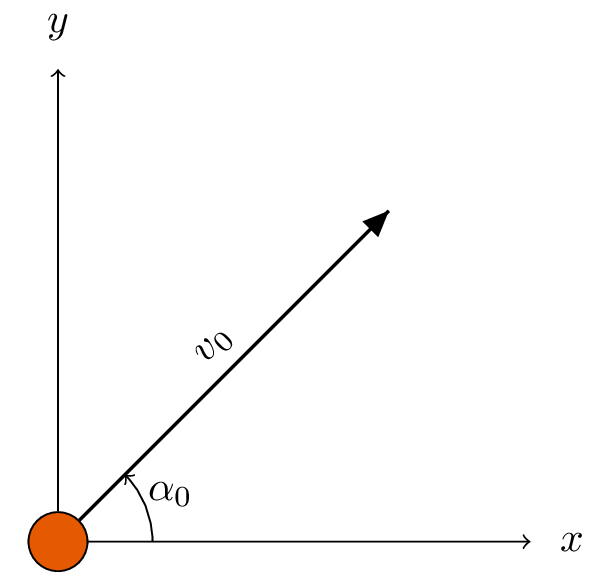
On utilise les notations suivantes :

$m$ est le poids du ballon en kg.
$v_0$ est la vitesse initiale (en $m.s^{-1}$) et $\alpha_0$ l’angle initial (en radian) par rapport à l’axe des abscisses.
$x(t)$, $y(t)$ est la position (en $m$) du ballon à l’instant $t$.
$v_x(t)$, $v_y(t)$ est la vitesse (en $m.s^{-1}$) du ballon à l’instant $t$, projeté sur l’axe des abscisses et des ordonnées.

On considère seulement la force de pesanteur sur le ballon.

Question

Appliquer le principe fondamental de la dynamique sur le ballon pour exprimer $x(t)$ et $y(t)$ en fonction de $v_0$, $\alpha_0$, $t$ et $g$ (champ de pesanteur terrestre).

Solution

D’après le PFD : $$m\vec{a} = m \vec{g}$$ En projetant le PFD sur les axes $x$ et $y$, on obtient :

\[\begin{align*} a_x &= 0\\ a_y &= -g \end{align*}\]

En intégrant :

\[\begin{align*} v_x(t) &= v_0 \cos(\alpha_0)\\ v_y(t) &= v_0 \sin(\alpha_0) - gt \end{align*}\]

En intégrant :

\[\begin{align*} x(t) &= v_0 \cos(\alpha_0) t\\ y(t) &= v_0 \sin(\alpha_0) t - \frac{1}{2}gt^2 \end{align*}\]

Dans la suite, on utilisera un pas $\Delta t = 0.01$ et $g = 9.81$.

Question

Écrire une fonction trajectoire(v0, a0) renvoyant deux listes x et y telles que x[k] et y[k] sont les coordonnées du ballon à l’instant $k \times \Delta t$. On arrêtera la trajectoire lorsque le ballon touche le sol.
On pourra utiliser np.cos et np.sin.

Solution

def trajectoire(v0, a0):
    x, y, t, dt, g = [0], [0], 0, 0.01, 9.81
    while y[-1] >= 0:
        t += dt
        x.append(v0*np.cos(a0)*t)
        y.append(v0*np.sin(a0)*t - .5*g*t**2)
    return x, y

x, y = trajectoire(10, np.pi/4)
x[:5], y[:5] # les 5 premières valeurs de x et y

([0,
07071067811865478,
14142135623730956,
2121320343559643,
2828427124746191],
 [0,
07022017811865475,
1394593562373095,
20771753435596427,
274994712474619])

Question

Tester avec le code ci-dessous.

def afficher_trajectoire(x, y):
    plt.clf()
    plt.plot(x, y, "k--", label="ballon")
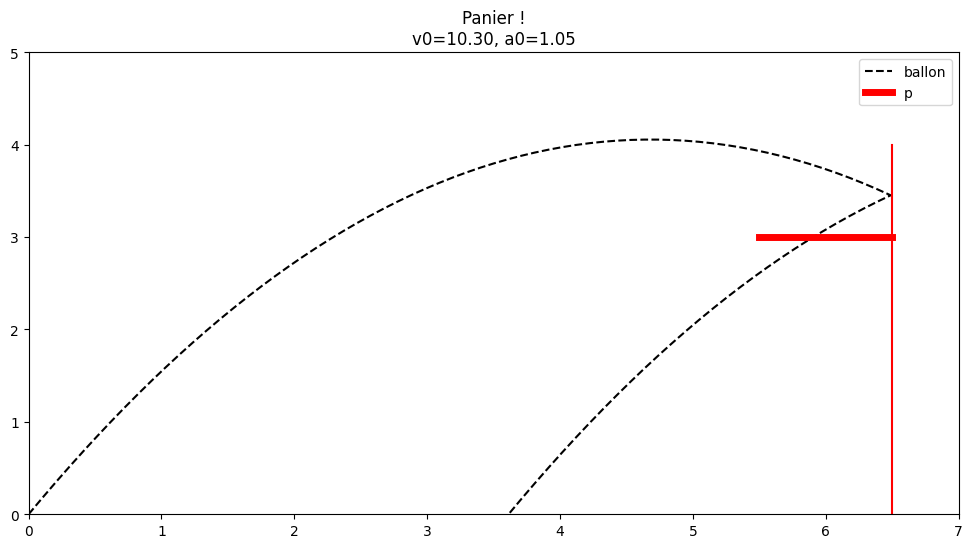
    plt.plot([p[0] - .5, p[0] + .5], [p[1], p[1]], c="r", lw=5, label="p")
    plt.plot([p[0] + .5]*2, [0, p[1] + 1], c="r")
    plt.legend()
    plt.xlim(0, p[0] + 1)
    plt.ylim(0, p[1] + 2)

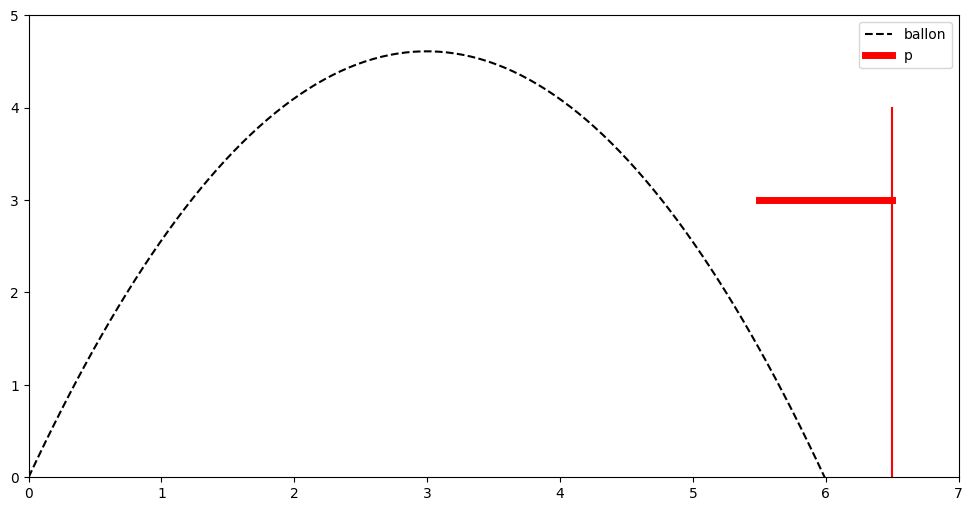
v0, a0 = 10, np.pi/2.5 # changer les valeurs de v0 et a0 pour changer la trajectoire
x, y = trajectoire(v0, a0)
afficher_trajectoire(x, y)
plt.show()

Question

Écrire une fonction resultat telle que, si x et y sont des listes correspondant à une trajectoire (comme renvoyé par trajectoire) et p les coordonnées du panier, resultat(x, y, p) renvoie 0 si le ballon rentre dans le panier, 1 si le ballon a été lancé trop fort et -1 s’il n’a pas été lancé assez fort.
Pour cela, on cherchera dans y un indice i tel que y[i] > p[1] et y[i+1] < p[1]. On considère que le ballon est rentré dans le panier si abs(x[i] - p[0]) < 0.5, que le ballon a été lancé trop fort si x[i] > p[0] et pas assez fort sinon.

Solution

def resultat(x, y, p):
    for i in range(len(x)):
        if y[i] > p[1] and y[i + 1] < p[1]:
            dx = x[i] - p[0]
            if abs(dx) < 0.5:
                return 0
            if dx > 0: return 1
            return -1
    return -1

resultat(x, y, p) # le ballon n'a pas été lancé assez fort

-1

Question

Tester avec la fonction ci-dessous. Modifier v0 pour marquer un panier.

def afficher(v0, a0, p):
    x, y = trajectoire(v0, a0)
    afficher_trajectoire(x, y)
    r = resultat(x, y, p)
    if r == 0:
        r = "Panier !"
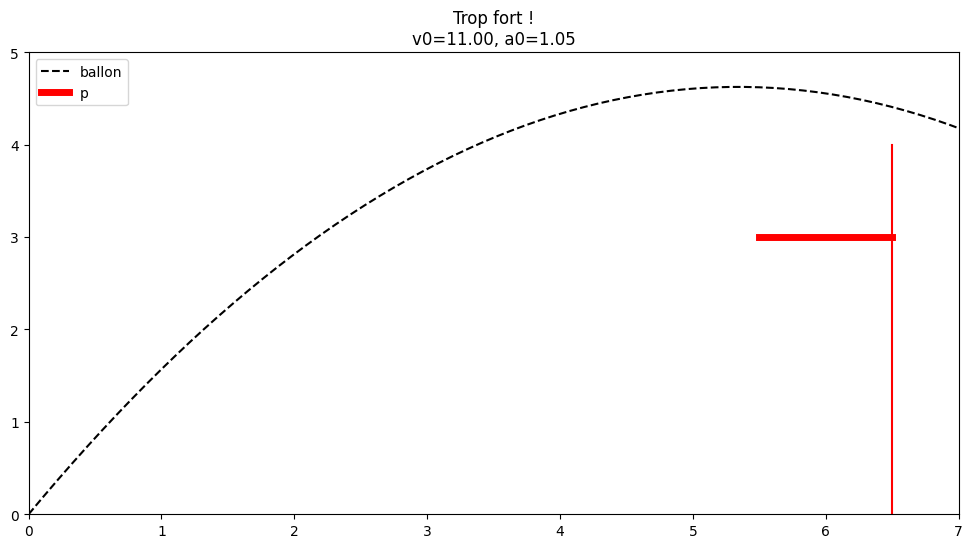
    elif r > 0:
        r = "Trop fort !"
    else:
        r = "Pas assez fort !"
    plt.title(f"{r}\nv0={v0:.2f}, a0={a0:.2f}")
    plt.show()

afficher(11, np.pi / 3, p)

Détermination de la vitesse initiale#

Recherche exhaustive#

Étant donné un angle $\alpha_0$ fixé, on veut déterminer une vitesse initiale $v_0$ permettant de marquer un panier.
Une première approche consiste à tester beaucoup de valeurs en espérant tomber sur un $v_0$ qui convient.

Question

Écrire une fonction brute(a0, p) qui teste toutes les valeurs de $v_0$ comprises entre 0 et 15 par pas de 0.01 et renvoie le premier $v_0$ qui permet de marquer un panier.

Solution

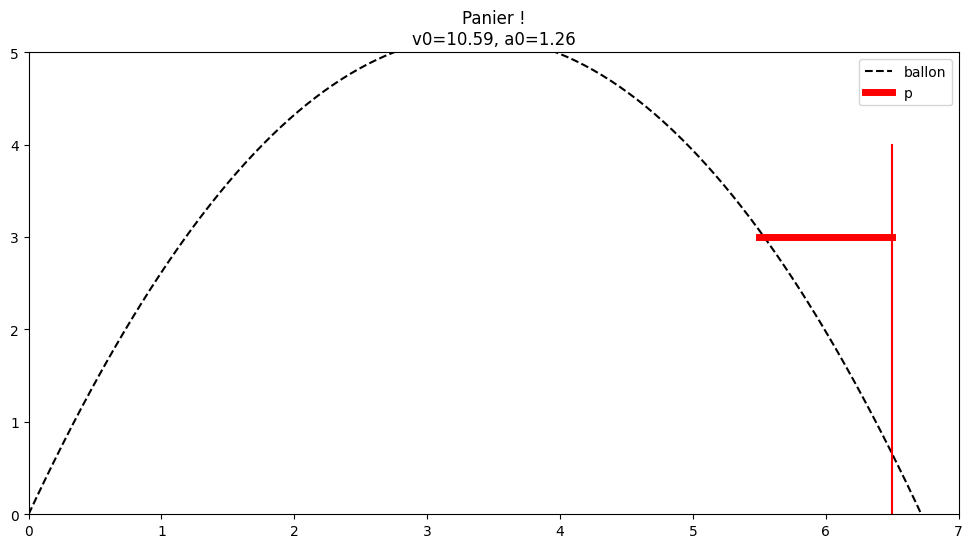
def brute(a0, p):
    for i in range(1500):
        v0 = i / 100
        if resultat(*trajectoire(v0, a0), p) == 0:
            return v0

afficher(brute(a0, p), a0, p)

Par dichotomie#

La recherche par dichotomie est plus efficace : on essaie une vitesse et on l’augmente ou la diminue en fonction du résultat.

Plus précisément, on conserve en mémoire deux variables $a$ et $b$ (initialement on prendra $a = 0$ et $b = 15$)) puis :

On calcule $v_0 = \frac{a + b}{2}$.
Si $v_0$ permet de marquer, on le renvoie.
Si $v_0$ était trop fort, on remplace $b$ par $v_0$ et on revient en 1.
Si $v_0$ n’était pas assez fort, on remplace $a$ par $v_0$ et on revient en 1.

Exercice

Ecrire une fonction dichotomie(a0, p) implémentant cet algorithme.

Solution

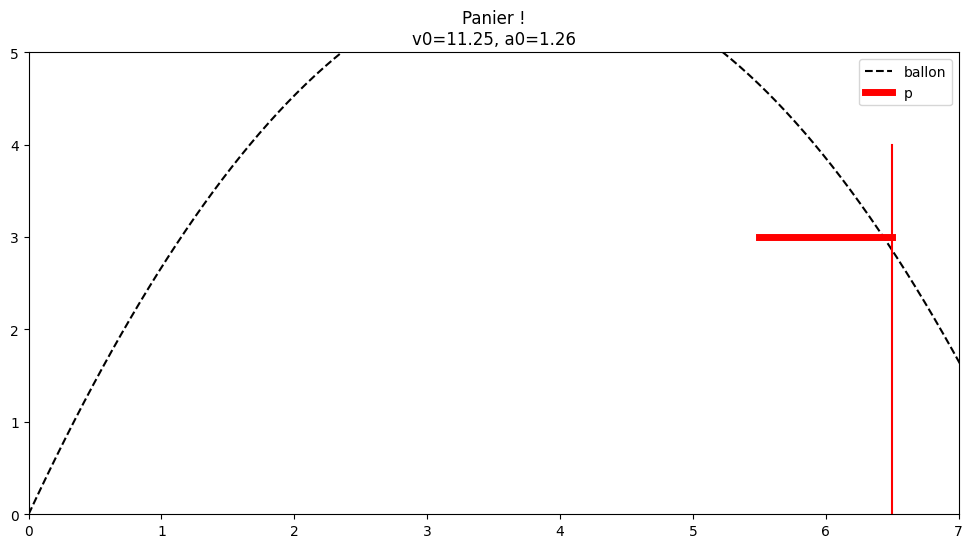
def dichotomie(a0, p):
    a, b = 0, 15
    while True:
        v0 = (a + b)/2
        x, y = trajectoire(v0, a0)
        r = resultat(x, y, p)
        if r == 0:
            return v0
        elif r < 0:
            a = v0
        else:
            b = v0

afficher(dichotomie(a0, p), a0, p)

Avec une équation#

Reprendre les équations de $x(t)$ et $y(t)$ que vous avez trouvé en première question du TP.

Question

Si $p_0$ et $p_1$ sont les coordonnées du panier, résoudre les équations suivantes d’inconnue $v_0$ :

\[\begin{split} x(t) = p_0\\ y(t) = p_1 \end{split}\]

Question

En déduire une fonction equation(a0, p) qui renvoie la vitesse initiale $v_0$ permettant de marquer un panier.

Solution

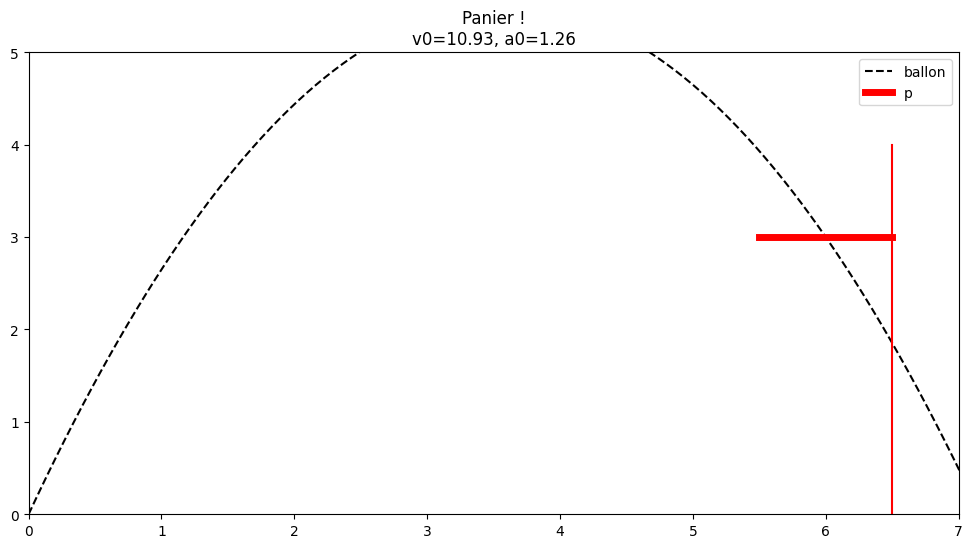
def equation(a0, p):
    return (9.81*p[0]**2/(2*(p[0]*np.tan(a0) - p[1])))**.5/np.cos(a0)

afficher(equation(a0, p), a0, p)

Panier avec rebond#

On veut maintenant gérer les rebonds sur le panneau. Pour cela on introduit une variable $s$ qui indique la direction dans laquelle le ballon se déplace : vers la droite si $s = 1$ et vers la gauche si $s = -1$. Initialement, $s = 1$ et $s$ devient égal à $-1$ en cas de rebond.
On calcule alors $x(t + \Delta t)$ avec l’équation de récurrence suivante :

\[ x(t + \Delta t) = x(t) + s \Delta t \times v_x(t) \]

Le calcul de $y(t)$ ne change pas (même code que trajectoire).

On pourra tester si le ballon en position $(x, y)$ touche le panneau du panier $p$ avec la fonction suivante :

def rebond(x, y, p):
    return p[0] + .45 < x < p[0] + .6 and y < p[1] + 1

Exercice

Écrire une fonction trajectoire2(v0, a0, p) renvoyant des listes x et y correspondant à la trajectoire du ballon, avec éventuellement un rebond sur le panneau du panier. On arrêtera la trajectoire lorsque le ballon touche le sol.

Tester ensuite avec la fonction ci-dessous.

Solution

def trajectoire2(v0, a0, p):
    x, y, t, dt, g = [0], [0], 0, 0.01, 9.81
    s = 1
    while y[-1] >= 0:
        t += dt
        x.append(x[-1] + s*v0*np.cos(a0)*dt)
        y.append(v0*np.sin(a0)*t - .5*g*t**2)
        if rebond(x[-1], y[-1], p):
            s = -1
    return x, y

def afficher2(v0, a0, p):
    x, y = trajectoire2(v0, a0, p)
    afficher_trajectoire(x, y)
    r = resultat(x, y, p)
    if r == 0:
        r = "Panier !"
    elif r > 0:
        r = "Trop fort !"
    else:
        r = "Pas assez fort !"
    plt.title(f"{r}\nv0={v0:.2f}, a0={a0:.2f}")
    plt.show()

afficher2(10.3, np.pi/3, p) # pour tester

Informatique en 2ème année de BCPST

TP 11 : Basketball

Contents

TP 11 : Basketball#

Trajectoire#

Détermination de la vitesse initiale#

Recherche exhaustive#

Par dichotomie#

Avec une équation#

Panier avec rebond#