TP 4 : Résolution d’équation différentielle par la méthode d’Euler#

La méthode d’Euler permet d’approximer une solution d’une équation différentielle.
Dans le TP, nous nous restreignons à une équation différentielle d’ordre $1$, c’est-à-dire où seules apparaissent des dérivées premières.

Commencez par importer les modules nécessaires :

import matplotlib.pyplot as plt
import numpy as np
plt.rcParams["figure.figsize"] = (15, 8)

Équation différentielle d’ordre 1#

Cadre général#

Considérons une équation différentielle d’ordre 1 :

\[\begin{align*} y'(t)& = f(t, y(t))\\ y(t_0)& = y_0 \end{align*}\]

$y$ est la fonction inconnue : on cherche à détermine la valeur de $y(t)$ pour $t \in I$, où $I \subseteq \mathbb{R}$ est l’intervalle de définition de $y$.
$f$ est l’expression qui apparaît dans le second membre de l’équation différentielle, qui peut utiliser $t$ et $y(t)$ (d’où une fonction de $2$ variables).
$y(t_0) = y_0$ est la condition initiale, garantissant l’unicité de la solution (théorème de Cauchy).

On cherche donc une fonction $y$ définie sur un intervalle $I$ telle que :

\[ \forall t \in I, \quad y'(t) = f(t, y(t)) \]

Exemples d’équations différentielles#

Voici des exemples d’équations différentielles classiques avec la valeur correspondante de $f(t, y)$ :

Équation différentielle	Second membre $f(t, y)$	Solution
$y'(t) = t$ $y(0) = 0$	$f(t, y) = t$	$y(t) = \frac{t^2}{2}$
$y'(t) = y(t)$ $y(0) = 1$	$f(t, y) = y$	$y(t) = e^t$
$y'(t) = \ln(t)$ $y(1) = -1$	$f(t, y) = \ln(t)$	$y(t) = t\ln(t) - t$

Exercice

Quelle fonction $f$ utiliser pour mettre l’équation différentielle $y'(t) = t^3 - y(t)^3$ sous la forme $y'(t) = f(t, y(t))$ ? Définir cette fonction en Python :

def f(t, y):
    return ... # utiliser y plutôt que y(t) ici

Solution

def f(t, y):
    return t**3 - y**3

Méthode d’Euler#

Théorie#

La méthode d’Euler calcule des approximations de $y$ de proche en proche. La valeur de $y(t_0) = y_0$ est connue (condition intiale).
Soit $h$ un petit réel (par exemple $0.01$) le pas d’approximation de la méthode d’Euler.

Alors, par développement limité d’ordre $1$ :

\[ y(t_0 + h) \approx y(t_0) + h y'(t_0) = y_0 + h y'(t_0) \]

Comme $y$ vérifie l’équation différentielle $y'(t_0) = f(t_0, y(t_0))$ :

\[ y(t_0 + h) \approx y_0 + hf(t_0, y(t_0)) \]

Ainsi, on peut approximer $y(t_0 + h)$ par $y_1 = y_0 + hf(t_0, y(t_0))$.

De même, on peut approximer $y(t_0 + 2h)$ par $y_1 + hf(t_0 + h, y_1)$, et ainsi de suite… Ce qui permet de définir des approximations $y_k \approx y(t_0 + kh)$ par la formule de récurrence suivante :

\[ \boxed{y_{k + 1} = y_k + h f(t_k, y_k)} \]

Où $t_k = t_0 + kh$.

Remarque : Cette dernière formule n’est autre que l’expression bien connue en physique $y(t + \Delta t) \approx y(t) + \Delta t \times y'(t)$, où on a remplacé $y'(t)$ par le second membre de l’équation différentielle.

Illustration#

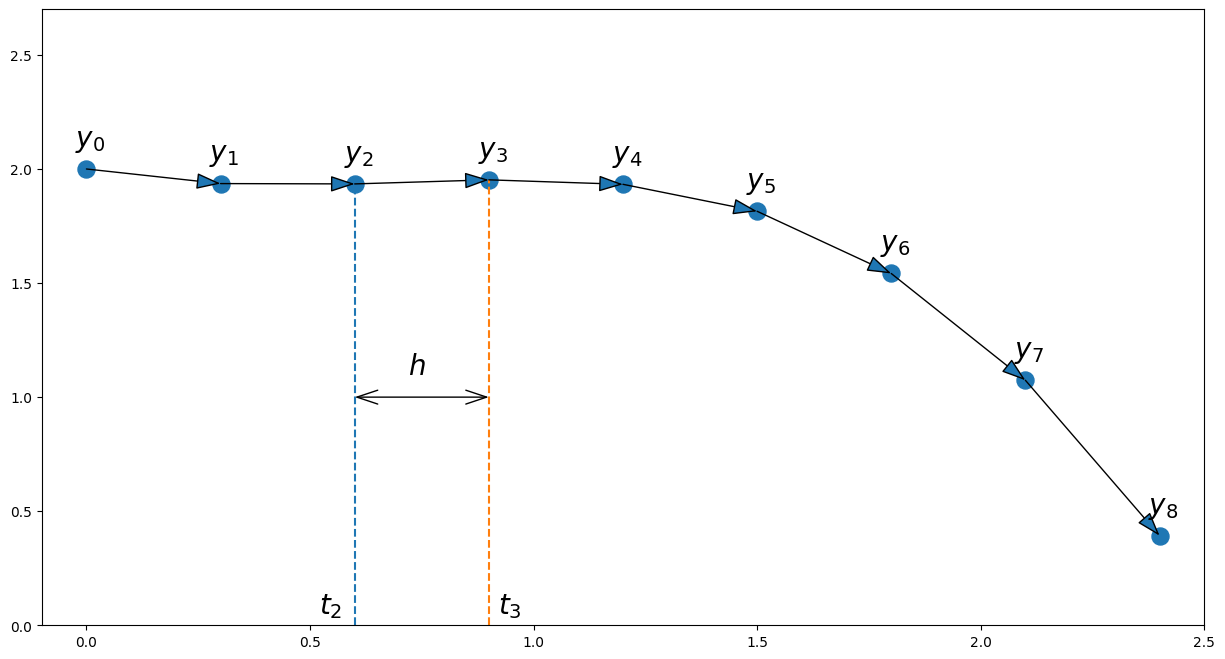
On obtient chaque point d’approximation en se déplaçant de $\Delta t$ le long de la tangente à $y$ :

def f(t, y):
    return np.cos(t)*t - 0.5

def arrow(p1, p2, double=False):
    a = "<->" if double else "-|>"
    plt.annotate("", 
        xytext=p1, 
        xy=p2, 
        arrowprops=dict(arrowstyle=f"{a},head_width=.5,head_length=1.5", 
            shrinkA=0,shrinkB=0))

t = [0]
y = [2]
h = 0.3
plt.axis([-0.1, 2.5, 0, 2.7])
for _ in range(10):
    t.append(t[-1] + h)
    y.append(y[-1] + h*f(t[-1], y[-1]))
    arrow((t[-2], y[-2]), (t[-1], y[-1]))

plt.scatter(t, y, s=150)
for i in range(len(t) - 1):
    plt.annotate(f"$y_{i}$", (t[i] - 0.025, y[i] + 0.1), fontsize=20)

plt.plot((t[2], t[2]), (0, y[2]), '--')
plt.plot((t[3], t[3]), (0, y[3]), '--')
plt.annotate("$t_2$", (t[2]-.08, 0.05), fontsize=20)
plt.annotate("$t_3$", (t[3]+.02, 0.05), fontsize=20)
plt.annotate(f"$y_{i}$", (t[i] - 0.025, y[i] + 0.1), fontsize=20)

arrow((t[2], 1), (t[3], 1), True)
plt.annotate("$h$", (t[2] + .4*h, 1.1), fontsize=20)

plt.show()

Programmation#

On calcule les approximations $y_k$ de $y$ en appliquant l’équation de récurrence $y_{k + 1} = y_k + h f(t_k, y_k)$ dans une boucle for.
Les approximations $y_k$ seront stockées dans une liste $y$ et les temps $t_k$ dans une liste $t$.

Voici un exemple d’équation différentielle avec le calcul des approximations par la méthode d’Euler :

\[\begin{align*} y'(t)& = y(t)\\ y(0)& = 1 \end{align*}\]

y = [1] # la première approximation est la condition initiale
t = [0] # temps initial
h = 0.01 # pas d'approximation
n = 200 # nombre d'approximations

for k in range(n):
    t.append(t[-1] + h)
    y.append(y[-1] + h*y[-1]) # équation de récurrence

En fait, on connaît la solution exacte de l’équation différentielle : $y(t) = e^t$. On peut donc comparer l’approximation avec la valeur exacte :

y[50] # approximation de exp(50*h) = exp(0.5)

1.644631821843882

np.exp(0.5)

1.6487212707001282

L’approximation est effectivement assez proche de la solution. Plus $h$ est petit, plus l’approximation est bonne mais plus cela prend du temps pour l’ordinateur.

Exercice

Quelle approximation de $e^1$ a été trouvée ? Comparer avec la vraie valeur.

Solution

print("approximation : ", y[100])
print("vraie valeur : ", np.exp(1))

On a calculé $n = 200$ approximations de l’équation différentielle $y'(t) = y(t)$. Comme $h = 0.01$, le dernier temps d’approximation est donc $0 + n\times h = 2$.

Exercice

Quel $n$ choisir pour approximer la solution sur $[0, 10]$ ?

Solution

Le dernier temps d’approximation est $n \times h$. Il faut choisir $n$ tel que $n \times h = 10$, c’est-à-dire $\boxed{n = 1000}$.

Exercice

De manière générale, donner la valeur de $n$ à choisir pour approximer une solution d’une équation différentielle sur un intervalle $[a, b]$ avec un pas de $h$.

Solution

\[ \boxed{n = \frac{b - a}{h}} \]

Affichage des approximations#

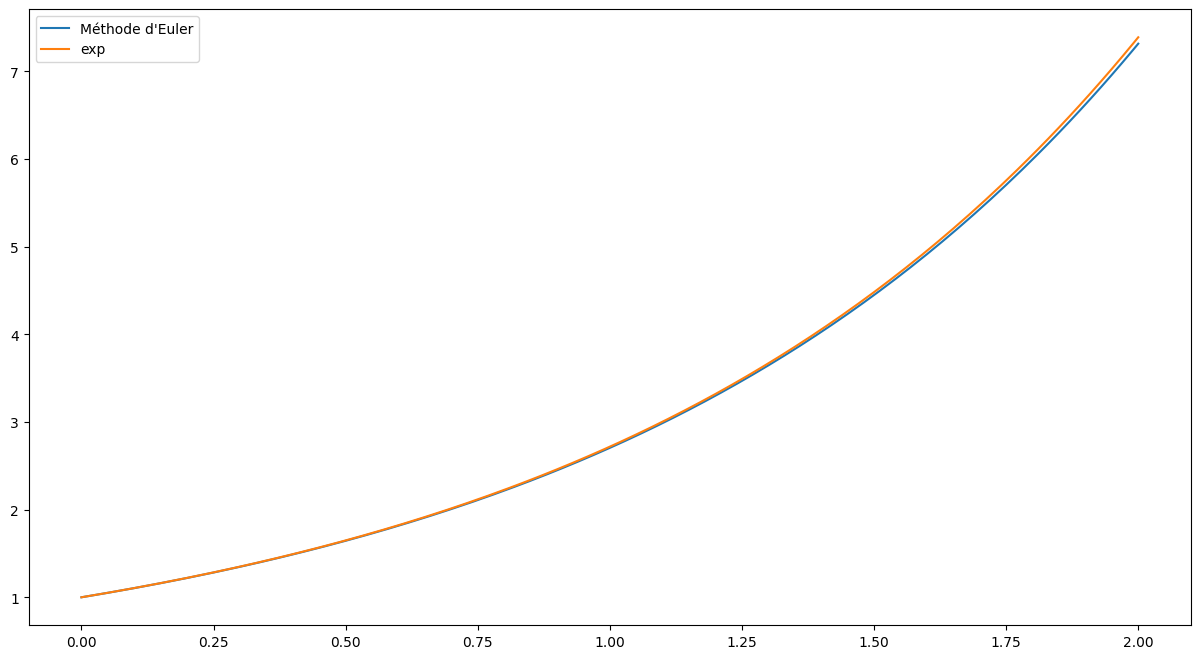
On peut afficher l’approximation obtenue, et la comparer avec la fonction exponentielle :

plt.plot(t, y, label="Méthode d'Euler")
plt.plot(t, np.exp(t), label="exp")
plt.legend()
plt.show()

Note

Si x et y sont deux listes, plt.plot(x, y) relie les points dont les abscisses sont dans x et les ordonnées dans y, ce qui revient à afficher y en fonction de x.

Exercice

Afficher la courbe d’une soluton approchée de $y'(t) = y(t)$ sur l’intervalle $[0, 3]$ (au lieu de $[0, 2]$ comme dans le dessin ci-dessus).

Solution

y = [1]
t = [0]
h = 0.01
n = 300 # on choisit n pour que n*h = 3

for k in range(n):
    t.append(t[-1] + h)
    y.append(y[-1] + h*y[-1]) # équation de récurrence
    
plt.plot(t, y, label="Méthode d'Euler")
plt.plot(t, np.exp(t), label="exp")
plt.legend()
plt.show()

<Figure size 1500x800 with 1 Axes>

Exercice

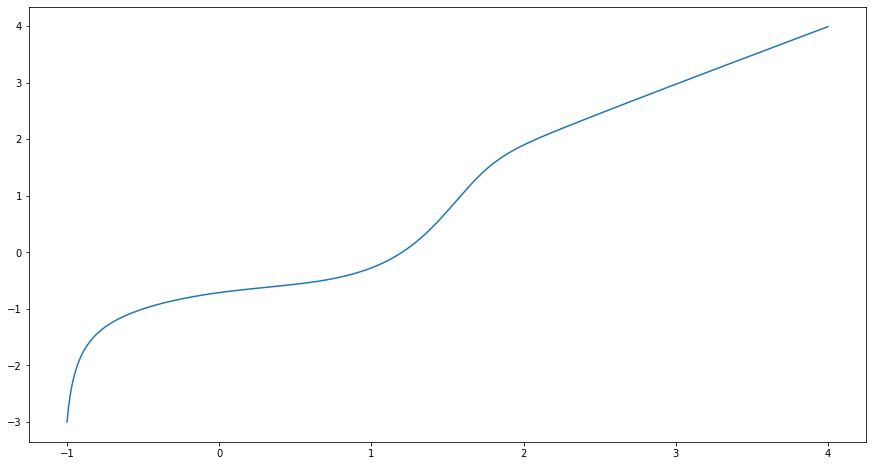
Résoudre de façon approchée l’équation différentielle ci-dessous, sur $[-1, 4]$, puis afficher la solution obtenue.

\[\begin{align*} y'(t)& = t^3 - y(t)^3\\ y(-1)& = -3 \end{align*}\]

On pourra adapter le code précédent ci-dessous.
Vous devez obtenir un dessin ressemblant à :

output

y = [...] # on met initialement la condition initiale
t = [...] # temps initial
h = 0.01 # pas d'approximation
n = ... # nombre d'approximations

for k in range(n):
    t.append(t[-1] + h)
    y.append(y[-1] + h*...) # équation de récurrence, où il faut remplacer ... par le membre droit de l'équa diff

Solution

y = [-3]
t = [-1]
h = 0.01
n = 500

for k in range(n):
    t.append(t[-1] + h)
    y.append(y[-1] + h*(t[-1]**3 - y[-1]**3))
    
plt.plot(t, y)
plt.show()

<Figure size 1500x800 with 1 Axes>

Méthode d’Euler générique#

La fonction suivante permet d’appliquer la méthode d’Euler avec les paramètres suivants :

f : fonction apparaissant dans le membre droit de l’équation différentielle.
t0 : temps initial.
y0 : valeur de la solution en t0 (condition initiale).
h : pas de l’approximation.
n : nombre d’approximations à calculer.

def euler(f, t0, y0, h, n):
    y = [y0]
    t = [t0]
    for k in range(n):
        t.append(t[-1] + h)
        y.append(y[-1] + h*f(t[-1], y[-1]))
    return t, y

f doit être définie comme une fonction classique en Python (avec def ...). On peut passer une fonction en argument à une autre fonction.

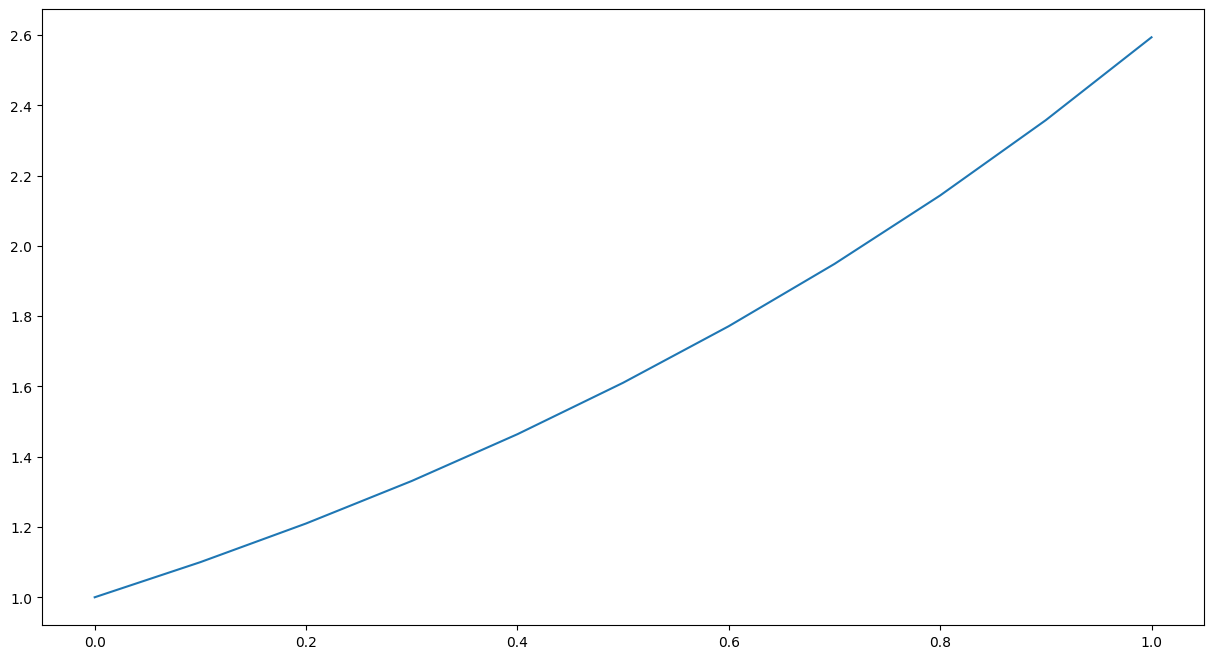
Par exemple, pour approcher une solution de $y'(t) = y(t)$ avec euler :

def f(t, y):
    return y

t, y = euler(f, 0, 1, 0.1, 10)
plt.plot(t, y)
plt.show()

Exercice

Dessiner des approximations de l’équation $y'(t) = t^3 - y(t)^3$ avec différentes conditions initiales : $y_0 = -3, y_0 = -2, y_0 = 0, y_0 = 4$.
On pourra utiliser euler dans une boucle for avec différentes valeurs de y_0 et utiliser plt.show() une seule fois, à la fin (après le for). Par exemple :

for y0 in [-3, -2, 0, 4]:
    ... # méthode d'Euler avec y0 comme condition initiale

Vous devez obtenir ce genre de dessin :

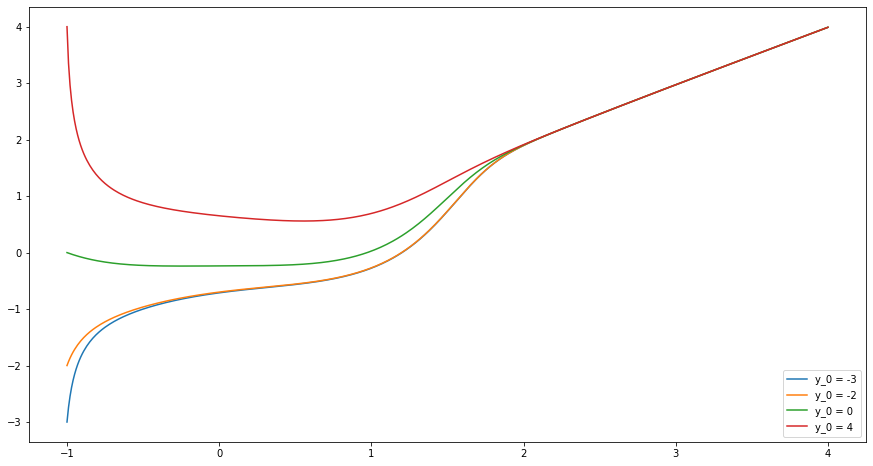
Solution

def f(t, y):
    return t**3 - y**3

for y0 in [-3, -2, 0, 4]:
    t, y = euler(f, -1, y0, 0.01, 500)
    plt.plot(t, y)

plt.show()

<Figure size 1500x800 with 1 Axes>

Système d’équations différentielles#

Il est également possible de résoudre un système d’équation différentielles.

Réactions chimiques#

Par exemple, considérons deux réactions chimiques d’ordre 1 : $$A \stackrel{\alpha}{\longrightarrow} B$$B \stackrel{\beta}{\longrightarrow} C$$

Les concentrations au cours du temps vérifient :

\[\begin{align*} \frac{d[A]}{dt}& = -\alpha [A] \\ \frac{d[B]}{dt}& = \alpha [A] - \beta [B]\\ \frac{d[C]}{dt}& = \beta [B] \end{align*}\]

\[ [A]_0 = 1, [B]_0 = 0, [C]_0 = 0 \]

Dans ce cas, on applique la méthode d’Euler sur chaque équation différentielle :

h = 0.05
t = [0]
A = [1]
B = [0]
C = [0]
for k in range(100): # approximations sur [0, 5]
    t.append(t[k] + h)
    A.append(A[k] + h*(-A[k])) # application de la méthode d'Euler sur chaque équation
    B.append(B[k] + h*(A[k] - B[k]))
    C.append(C[k] + h*B[k])

plt.plot(t, A, 'r', label="[A]")
plt.plot(t, B, 'b', label="[B]")
plt.plot(t, C, 'g', label="[C]")
plt.legend()
plt.show()

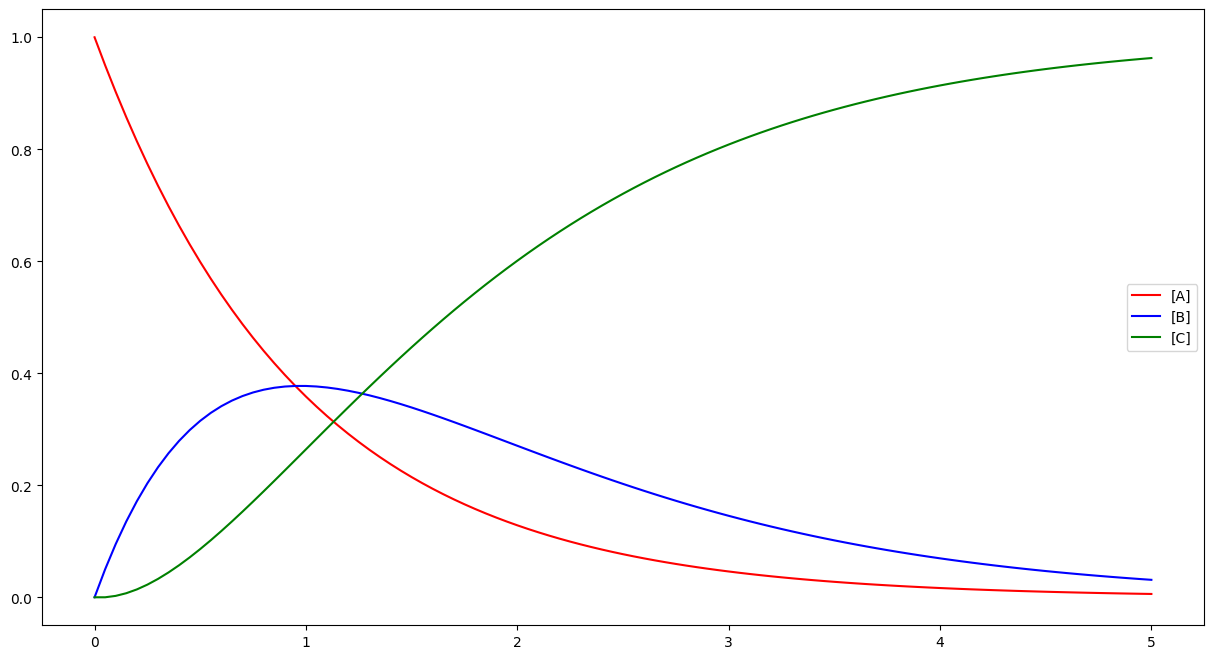
Exercice

Interpréter le dessin ci-dessus.

Solution

La concentration de A diminue puisque A se transforme en B.
B augmente initialement (résultant de la production à partir de A) mais diminue ensuite (car se transforme en C).
À la fin, il n’y a plus que du C.

Évolution de population (Lokta-Volterra)#

Le système différentiel de Lotka-Volterra permet de modéliser l’évolution conjointe de populations de proies et de prédateurs :

\[\begin{align*} x'(t)& = x(t) \, \bigl(\alpha - \beta \, y(t) \bigr) \\ y'(t)& = y(t) \, \bigl(\delta \, x(t) - \gamma \bigr) \end{align*}\]

$x(t)$ : la population de proies au temps $t$;
$y(t)$ : la population de prédateurs au temps $t$;
$\alpha$ : le taux de reproduction des proies indépendamment des prédateurs rencontrés;
$\beta$ : le taux de mortalité des proies dues aux prédateurs rencontrés;
$\gamma$ : le taux de mortalité des prédateurs indépendamment du nombre de proies
$\delta$ : le taux de reproduction des prédateurs en fonction des proies mangées.

Exercice

Écrire les équations de récurrences vérifiées par les approximations $x_k$ et $y_k$ de la méthode d’Euler, appliquée au système différentiel ci-dessus.
Écrire des instructions Python pour stocker dans des listes t, x et y ces $t_k$, $x_k$ et $y_k$. On choisira l’intervalle de temps et le nombre d’approximations judicieusement et on prendra $\alpha = \beta = \gamma = \delta = 1$.
Afficher $y$ en fonction de $x$ et interpréter.
Afficher $y$ en fonction de $t$ et $x$ en fonction de $t$, sur le même dessin et interpréter.
Essayer de modifier les constantes $\alpha$, $\beta$…

Solution

a = b = c = d = 1
x = [1]
y = [2]
t = [0]
h = 0.01

for k in range(2000):
    t.append(t[-1] + h)
    x.append(x[-1] + h*x[-1]*(a - b*y[-1]))
    y.append(y[-1] + h*y[-1]*(c*x[-1] - d))
    
plt.plot(t, x)
plt.plot(t, y)
plt.show()

<Figure size 1500x800 with 1 Axes>

Équation du second ordre#

Pour résoudre une équation différentielle d’ordre 2 du type $y'' = f(t, y, y')$, on peut poser $z(t) = y'(t)$ pour se ramener à un système de 2 équations différentielles d’ordre 1 dont les inconnues sont $y$ et $z$.

Par exemple, calculons une solution approchée de l’équation du pendule linéarise :

\[ \theta''(t) = -\theta(t) \]

Cette équation est du second ordre, donc on ne peut pas appliquer directement la méthode d’Euler.
Par contre, si on pose $z(t) = \theta'(t)$ alors, comme $z'(t) = \theta''(t) = -\theta(t)$ (d’après pendule) on peut réécrire cette équation du second ordre comme deux équations du premier ordre :

\[\begin{align*} \theta'(t)& = z(t)\\ z'(t)& = -\theta(t) \end{align*}\]

On applique alors la méthode d’Euler sur chaque équation, comme dans la section précédente :

h = 0.01
theta = [0]
z = [1]
t = [0]

for k in range(1000):
    t.append(t[k] + h)
    theta.append(theta[k] + h*z[k])
    z.append(z[k] - h*theta[k])

plt.plot(t, theta)
plt.show()

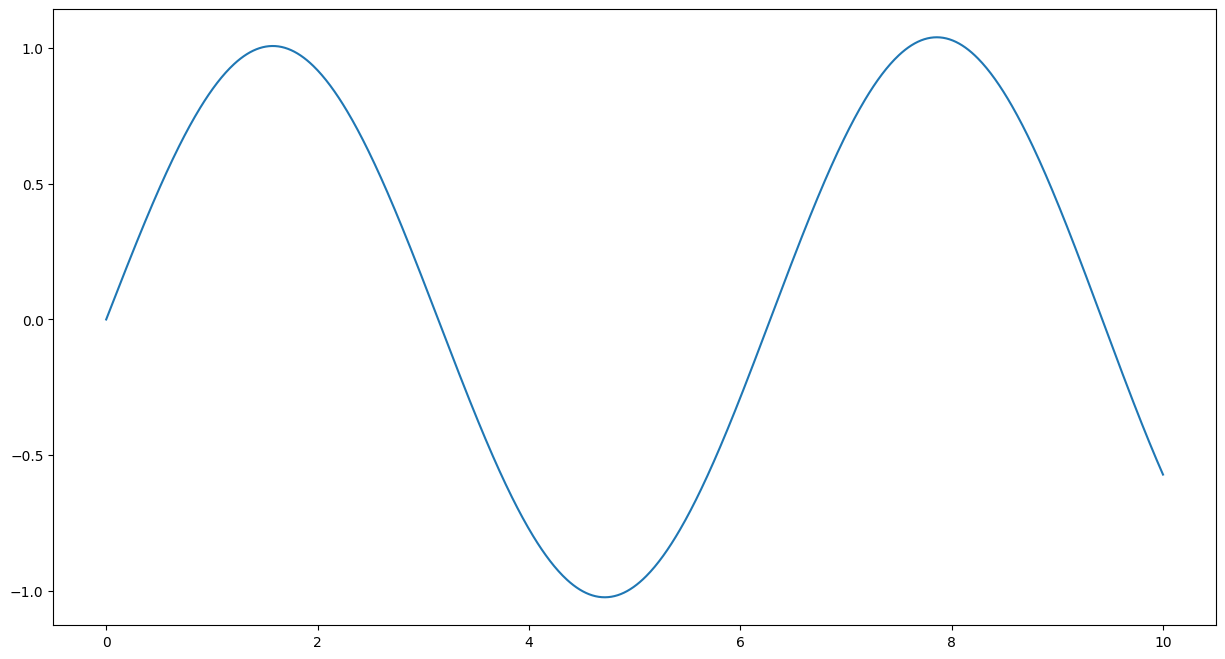
Exercice

Quelle est la courbe obtenue ?

Solution

On sait résoudre l’équation différentielle : les solutions sont de la forme $\theta(t) = A \cos(t) + B \sin(t)$.
Comme $\theta(0)$ = 0, $A = 0$.
Comme $\theta'(0)$ = 1, $B = 1$.
Donc $\boxed{\theta(t) = \sin(t)}$.

Exercice

Adapter la résolution ci-dessus pour l’équation du pendule non-linéarise $\theta''(t) = -\sin(\theta(t))$. Interpréter le dessin.

Solution

h = 0.005
theta = [0]
z = [1]
t = [0]

for k in range(10000):
    t.append(t[k] + h)
    theta.append(theta[k] + h*z[k])
    z.append(z[k] - h*np.sin(theta[k])) # changement

plt.plot(t, theta)
plt.show()

<Figure size 1500x800 with 1 Axes>

Équation différentielle	Second membre \(f(t, y)\)	Solution
\(y'(t) = t\) \(y(0) = 0\)	\(f(t, y) = t\)	\(y(t) = \frac{t^2}{2}\)
\(y'(t) = y(t)\) \(y(0) = 1\)	\(f(t, y) = y\)	\(y(t) = e^t\)
\(y'(t) = \ln(t)\) \(y(1) = -1\)	\(f(t, y) = \ln(t)\)	\(y(t) = t\ln(t) - t\)

Informatique en 2ème année de BCPST

TP 4 : Résolution d’équation différentielle par la méthode d’Euler

Contents

TP 4 : Résolution d’équation différentielle par la méthode d’Euler#

Équation différentielle d’ordre 1#

Cadre général#

Exemples d’équations différentielles#

Méthode d’Euler#

Théorie#

Illustration#

Programmation#

Affichage des approximations#

Méthode d’Euler générique#

Système d’équations différentielles#

Réactions chimiques#

Évolution de population (Lokta-Volterra)#

Équation du second ordre#