TP 5 : Dessins, récursivité et fractales#

Turtle#

Le module turtle de Python permet de tracer des figures, comme on le ferait avec un stylo.
La “tortue” (pointe du stylo) est initialement placée à l’origine d’un repère, la “tête” orientée à droite, et se déplace sur le graphique en fonction des instructions qu’on lui donne.

Les principales instructions sont les suivantes :

Instruction

Effet

forward(n) ou fd(n)

avance de n pixels

left(n) ou lt(n)

effectue une rotation à gauche de n degrés

right(n) ou rt(n)

effectue une rotation à droite de n degrés

reset()

efface l’écran

done()

affiche le dessin (à faire à la fin)

color(c)

utilise la couleur c pour dessiner (exemple : color("red"))

Question

Importer le module turtle avec l’instruction from turtle import *.

Solution

#1
from turtle import *

Question

Tester avec le code suivant, qui avance la tortue de \(100\) pixels, puis tourne de \(40\) degrés à gauche, puis avance de \(200\) pixels.
Remarque : si vous avez une erreur Terminator ..., essayez de relancer le code.

reset()
fd(100)
left(40)
fd(200)
done()

Question

Écrire une fonction carre(n) qui trace un carré de côté n pixels.

Solution

def carre(n):
    reset()
    fd(n)
    left(90)
    fd(n)
    left(90)
    fd(n)
    left(90)
    fd(n)
    done()

carre(100)

Question

Écrire une fonction triangle(n) qui trace un triangle équilatéral de côté n pixels.

Solution

def triangle(n):
    reset()
    fd(n)
    left(120)
    fd(n)
    left(120)
    fd(n)
    done()

triangle(100)

Question

Écrire une fonction polygone(k, n) affichant un polygone régulier à k côtés, chaque côté étant de longueur n.

Solution

def polygone(k, n):
    reset()
    for i in range(k):
        fd(n)
        left(360/k)
    done()

polygone(6, 100)

Question

Écrire une fonction carres affichant des carrés évoluant en spirale, comme ci-dessous. On pourra utiliser speed(10) pour dessiner rapidement.

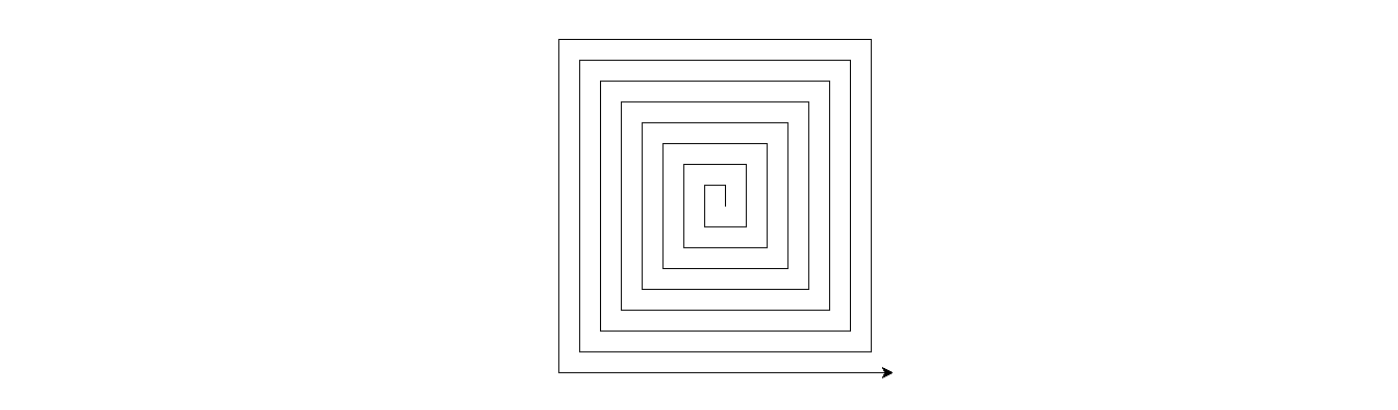
Solution

def carres(n, larg):
    reset()
    speed(10)
    for i in range(1, n+1):
        largeur = larg * i
        left(90)
        fd(largeur)
        left(90)
        fd(largeur)
    done()

Question

Reprendre la fonction précédente pour que le tracé se fasse en bleu pour la partie supérieure droite et en rouge pour la partie inférieure gauche.

Solution

#3
def carres_couleurs(n, larg):
    reset()
    speed(10)        # vitesse 8 sur une échelle de 1 à 10
    couleurs = ['red', 'blue']
    for i in range(1, n+1):
        largeur = larg * i
        color(couleurs[i % 2])        # tracé en rouge lorsque i est pair, en violet sinon
        left(90)
        fd(largeur)
        left(90)
        fd(largeur)
    done()

Récursivité#

On dit qu’une fonction est récursive si elle s’appelle elle-même. Par exemple, considérons la fonction suivante :

def f(n):
    if n == 0:
        return 0
    return n + f(n - 1)

On voit que f(n) appelle f(n - 1) si n est différent de 0. L’exécution de f(n) se met alors en pause et f(n - 1) s’exécute. Une fois que f(n - 1) reprend, f(n) continue son exécution.

Question

Sans exécuter f(n), essayer de deviner ce que va renvoyer f(1), f(2), f(3), f(5).

Question

Vérifier votre réponse à la question précédente en exécutant f(n).

Question

Conjecturer la valeur de retour de f(n) en fonction de n. Par quel type de méthode mathématiques pourrait-on prouver ce résultat ?

Question

Exprimer \(n!\) en fonction de \((n - 1)!\) et en déduire une fonction récursive fact(n) renvoyant \(n!\).
Remarque : fact(n) ressemble beaucoup à f(n)…

Flocon de Von Koch#

Un flocon de Von Koch s’obtient en partant d’un triangle équilatéral, puis en modifiant successivement chaque arête de la façon suivante :

  • On divise l’arête en 3

  • On construit un triangle équilatéral ayant pour base le segment du milieu

  • On ôte le segment du milieu

  • On effectue de nouveau ces étapes sur chacune des arêtes obtenues

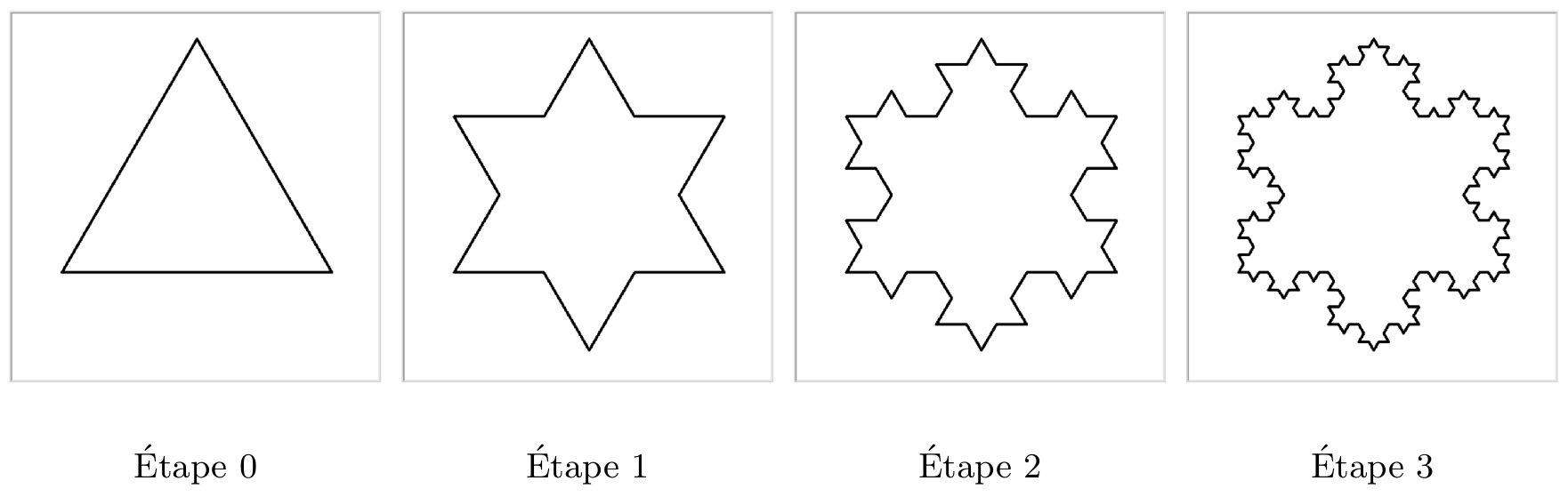
Question

Écrire une fonction branche telle que branche(largeur, n) construit l’un des trois côtés d’un flocon jusqu’à l’étape n, de la largeur souhaitée. Cette fonction doit être récursive. En effet, pour construire une branche jusqu’à l’étape n, il faut construire 4 motifs jusqu’à l’étape n-1 :

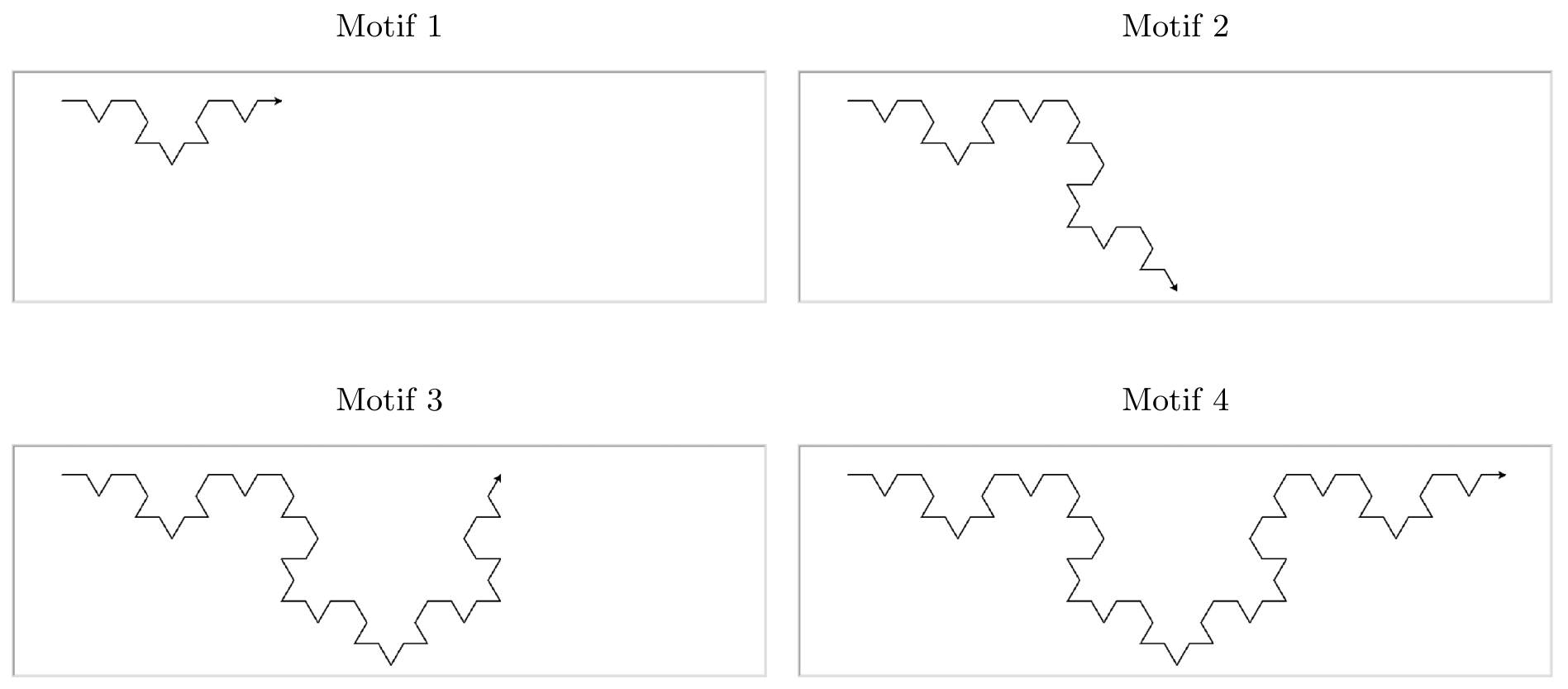
Vous pourrez compléter le code de branche ci-dessous (sans mettre de reset() ni done() à l’intérieur) :

def branche(largeur, n):
    if n == 0: # cas de base : on dessine juste un trait 
        ...
    else:
        ... # appel récursif pour construire le motif 1
        ... # changer l'orientation de la tortue
        ... # appel récursif pour construire le motif 2
        ... # changer l'orientation de la tortue
        ... # appel récursif pour construire le motif 3
        ... # changer l'orientation de la tortue
        ... # appel récursif pour construire le motif 4

Solution

#1
def branche(largeur, n):
    if n == 0:
        fd(largeur)    # à l'étape 0 on trace un simple trait
    else:
        branche(largeur / 3, n-1)    # construction du motif 1
        right(60)
        branche(largeur / 3, n-1)    # construction du motif 2
        left(120)
        branche(largeur / 3, n-1)    # construction du motif 3
        right(60)
        branche(largeur / 3, n-1)    # construction du motif 4

reset()
branche(300, 3)
done()

Question

Écrire une fonction flocon telle que flocon(largeur, n) construit un flocon jusqu’à l’étape n, avec une largeur de base largeur.

Solution

#2
def flocon(largeur, n):
    reset()
    pensize(2)        # fixe l'épaisseur du trait
    speed(0)        # accélère le tracé
    branche(largeur, n)        # côté 1
    left(120)
    branche(largeur, n)        # côté 2
    left(120)
    branche(largeur, n)        # côté 3
    hideturtle()        # fait disparaître la tortue
    done()

flocon(260, 4)

Si vous avez terminé, faites ce TP qui est sur le même thème (fractales).

Solution

def tree(l, n):
    if n != 0:
        fd(l)
        right(30)
        tree(l * 0.8, n - 1)
        left(60)
        tree(l * 0.8, n - 1)
        right(30)
        bk(l)
reset()
speed(0)
tree(100, 10)
done()