TP 6 : Application aux mathématiques#

Nombres complexes#

Dans cet exercice, un nombre complexe est représenté par un couple \((a, b)\) avec \(a\) la partie réelle et \(b\) la partie imaginaire.
On rappelle que si z est un couple, alors on peut obtenir le \(i\)ème élément de z avec z[i].

Question

Écrire une fonction conjugue(z) qui renvoie le complexe conjugué de z.

Solution

def conjugue(z):
    return (z[0], -z[1])

conjugue((1, 2))

(1, -2)

Question

Écrire une fonction module(z) qui renvoie le module du nombre complexe z.

Solution

def module(z):
    return (z[0]**2 + z[1]**2)**0.5

module((3,4))

5.0

Question

Écrire une fonction somme(z1, z2) qui renvoie la somme des nombres complexes z1 et z2.

Solution

def somme(z1, z2):
    return (z1[0] + z2[0], z1[1] + z2[1])

somme((1, 2), (3, 4))

(4, 6)

Question

Écrire une fonction produit(z1, z2) qui renvoie le produit des nombres complexes z1 et z2.

Solution

def produit(z1, z2):
    return (z1[0]*z2[0] - z1[1]*z2[1], z1[0]*z2[1] + z1[1]*z2[0])

produit((3,4), (5,6))

(-9, 38)

Question

Écrire une fonction puissance(z, n) qui renvoie le nombre complexe z à la puissance n.

Solution

def puissance(z, n):
    if n == 0:
        return (1, 0)
    else:
        return produit(z, puissance(z, n-1))

puissance((3,4), 3)

(-117, 44)

Question

Écrire une fonction fraction(z1, z2) qui renvoie le quotient des nombres complexes z1 et z2. Il faut donc mettre ce nombre sous la forme d’un nombre complexe \(a + ib\).
On pourra calculer à la main \(\frac{a_1 + ib_1}{a_2 + ib_2}\) en multipliant par la quantité conjuguée.

Solution

def fraction(z1, z2):
    a, b = produit(z1, (z2[0], -z2[1]))
    m = module(z2)**2
    return (a/m, b/m)

fraction((3,4), (5,6))

(0.639344262295082, 0.03278688524590164)

Vecteurs#

Un vecteur est représenté par une liste de nombres. Par exemple, le vecteur \(\begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}\) est représenté par la liste [1, 2, 3].

Question

Écrire une fonction norme(v) qui renvoie la norme du vecteur v. On rappelle que la norme (euclidienne) d’un vecteur \(v = \begin{pmatrix} v_1 \\ v_2 \\ \vdots \\ v_n \end{pmatrix}\) est donnée par \(\sqrt{v_1^2 + v_2^2 + \cdots + v_n^2}\).

Solution

def norme(v):
    n = 0
    for x in v:
        n += x**2
    return n**0.5

norme([1, 2, 3])

3.7416573867739413

Question

Écrire une fonction produit_scalaire(v1, v2) qui renvoie le produit scalaire des vecteurs v1 et v2.

Solution

def produit_scalaire(v1, v2):
    s = 0
    for i in range(len(v1)):
        s += v1[i]*v2[i]
    return s

produit_scalaire([1, 2, 3], [4, 5, 6])

Question

Écrire une fonction orthogonaux(v1, v2) qui renvoie True si les vecteurs v1 et v2 sont orthogonaux et False sinon.
Remarque :

On peut utiliser la fonction produit_scalaire pour écrire cette fonction.
Si x est un float, il ne faut pas tester si x == 0 mais plutôt abs(x) < 1e-10, car les calculs sur les nombres flottants sont approchés (erreurs d’arrondis).

Solution

def orthogonaux(v1, v2):
    return produit_scalaire(v1, v2) < 1e-10

orthogonaux([1, 0], [0, 1])

True

Polynômes#

Dans cet exercice, tous les polynômes sont représentés par une liste de coefficients : un polynôme \(P = a_0 + a_1 X + ... + a_n X^n\) est représenté par la liste \([a_0, a_1, \ldots, a_n]\) où \(a_i\) est le coefficient de \(X^i\).
Par exemple, \(-2 + 7X^2 + X^3\) est représenté par la liste [-2, 0, 7, 1].

Question

Écrire une fonction degre(P) qui renvoie le degré d’un polynôme P (représenté par une liste).

Solution

def degre(P):
    return len(P)-1

degre([-2, 0, 7, 1])

Question

Écrire une fonction evaluer(P, x) qui renvoie la valeur \(P(x)\) du polynôme P en x.

Solution

def evaluer(P, x):
    px = 0
    for i in range(len(P)):
        px += P[i] * x**i
    return px

evaluer([-2, 0, 7, 1], 2) # P(2)

Question

Écrire une fonction derivee(P) qui renvoie la dérivée du polynôme P.

Solution

def derivee(P):
    dP = []
    for i in range(1, len(P)):
        dP.append(P[i] * i)
    return dP

derivee([-2, 0, 7, 1]) # P'(x) = 14X + 3X^2

[0, 14, 3]

Question

Écrire une fonction somme(P, Q) qui renvoie la somme de deux polynômes P et Q.

Solution

def somme(P, Q):
    PQ = []
    for i in range(max(len(P), len(Q))):
        if i < len(P):
            if i < len(Q):
                PQ.append(P[i] + Q[i])
            else:
                PQ.append(P[i])
        else:
            PQ.append(Q[i])
    return PQ

somme([-2, 0, 7, 1], [1, 2, 3])

[-1, 2, 10, 1]

Question

Écrire une fonction produit(P, Q) qui renvoie le produit R de deux polynômes P et Q. On rappelle que, si \(P(X) = \sum a_k X^k\) et \(Q(X) = \sum b_k X^k\), alors \(R(X) = \sum c_k X^k\) où \(c_k = \sum_{i+j=k} a_i b_j\).
On pourra commencer par créer une liste R contenant \(\deg(P) + \deg(Q) + 1\) zéros et, pour chaque coefficient \(a_i\) de \(P\) et \(b_j\) de \(Q\), ajouter \(a_i b_j\) à \(R[i+j]\).

Solution

def produit(P, Q):
    R = []
    for i in range(len(P) + len(Q) - 1):
        R.append(0)
    for i in range(len(P)):
        for j in range(len(Q)):
            R[i+j] += P[i] * Q[j]
    return R

produit([-2, 0, 7, 1], [1, 2, 3])

[-2, -4, 1, 15, 23, 3]

Intégrale#

La méthode des rectangles est une façon d’approximer une intégrale \(\int_a^b f(x) \, dx\) par la somme des aires de \(n\) rectangles de largeur \(h = \frac{b-a}{n}\) :

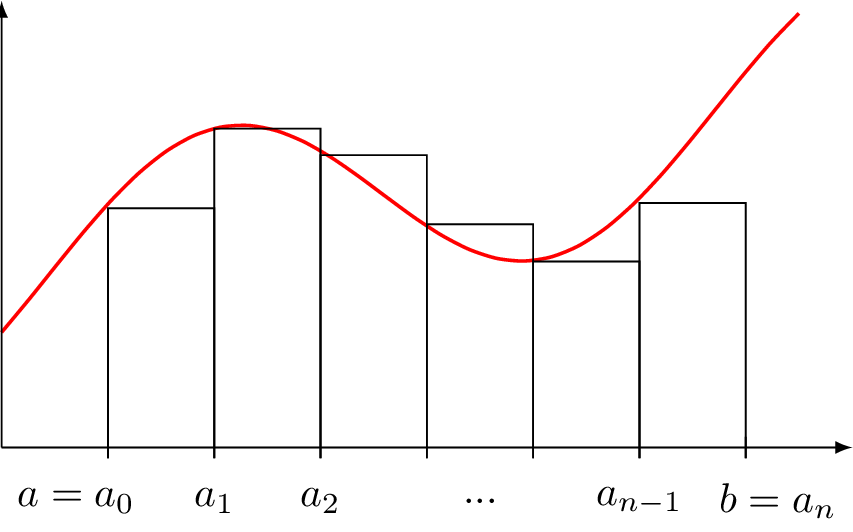
\[ \int_a^b f(x) \, dx \approx \sum_{i=0}^{n-1} \underbrace{f(a + ih) \, h}_{\text{aire d'un rectangle}} \]

Question

Écrire une fonction methode_rectangle(f, a, b, n) qui renvoie l’approximation de l’intégrale \(\int_a^b f(x) \, dx\) en utilisant la formule ci-dessus. Tester avec une fonction carre (à définir) et vérifier à la main.

Solution

def methode_rectangle(f, a, b, n):
    h = (b-a)/n
    s = 0
    for i in range(n):
        s += f(a + i*h)
    return s*h

def carre(x):
    return x**2

methode_rectangle(carre, 0, 1, 100)

0.32835000000000003

Méthode du pivot de Gauss#

On veut résoudre un système linéaire de \(n\) équations à \(n\) inconnues de la forme :

\[\begin{split} \text{(S): }\left\lbrace\begin{array}{c} a_{1,1} \; x_1 +\cdots +a_{1,n} \; x_n=b_1 \\ \cdots \\ a_{n,1} \; x_1 +\cdots +a_{n,n} \; x_n=b_n \end{array} \right. \end{split}\]

On commence par réécrire ces équations sous forme matricielle :

\[ (S)\Leftrightarrow AX=B \]

\[\begin{split} \text{avec} \quad A=\begin{pmatrix} a_{1,1} & a_{1,2} & \cdots & a_{1,n} \\ a_{2,1} & a_{2,2} & \cdots & a_{2,n} \\ \cdots & \cdots & \cdots & \cdots \\ a_{n,1} & a_{n,2} & \cdots & a_{n,n} \end{pmatrix} \text{,} \quad X=\begin{pmatrix} x_1 \\ x_2 \\ \cdots \\ x_n \end{pmatrix} \quad\text{et} \quad B=\begin{pmatrix} b_1 \\ b_2 \\ \cdots \\ b_n \end{pmatrix} \end{split}\]

Il est pratique de considérer la matrice augmentée du système :

\[\begin{split} M = (A\vert B)=\begin{pmatrix} a_{1,1} & a_{1,2} & \cdots & a_{1,n} & b_1 \\ a_{2,1} & a_{2,2} & \cdots & a_{2,n} & b_2 \\ \cdots & \cdots & \cdots & \cdots & \cdots \\ a_{n,1} & a_{n,2} & \cdots & a_{n,n} & b_n \end{pmatrix} \end{split}\]

Dans la suite, on pourra tester avec la matrice suivante :

import numpy as np

M = np.array([[-2.0,4.0,1.0,-18.0],[8.0,2.0,-1.0,6.0],[2.0,-1.0,2.0,27.0]])
M

array([[ -2.,   4.,   1., -18.],
       [  8.,   2.,  -1.,   6.],
       [  2.,  -1.,   2.,  27.]])

La méthode du pivot de Gauss utilise des opérations élémentaires sur matrice : dilatation, échange, transvection.

Question

Écrire une fonction dilatation telle que dilatation(M, i, a) multiplie la ligne i de la matrice M par a, c’est à dire l’opération \(L_i \leftarrow a L_i\).

Solution

def dilatation(M, i, l):
    M[i] = l*M[i] 

dilatation(M, 0, 2)
M

array([[ -4.,   8.,   2., -36.],
       [  8.,   2.,  -1.,   6.],
       [  2.,  -1.,   2.,  27.]])

Question

Écrire une fonction echange(M, i, j) qui échange les lignes i et j de la matrice M, c’est à dire l’opération \(L_i \leftrightarrow L_j\).

Solution

def echange(M, i, j):
    M[i], M[j] = M[j].copy(), M[i].copy()

echange(M, 0, 1)
M

array([[  8.,   2.,  -1.,   6.],
       [ -4.,   8.,   2., -36.],
       [  2.,  -1.,   2.,  27.]])

Question

Écrire une fonction transvection telle que transvection(M, i, j, a) ajoute à la ligne i de la matrice M la ligne j multipliée par a, c’est à dire l’opération \(L_i \leftarrow L_i + a L_j\).

Solution

def transvection(M, i, j, l):
    M[i] = M[i] + l * M[j]

transvection(M, 0, 1, 2)
M

array([[  0.,  18.,   3., -66.],
       [ -4.,   8.,   2., -36.],
       [  2.,  -1.,   2.,  27.]])

Exercice

Écrire une fonction pivot telle que pivot(M, j) renvoie un pivot sur la jème colonne, c’est à dire un indice \(i \geq j\) tel que l’élément \(m_{i, j}\) de M soit non nul.

Solution

def pivot(M, j):
    for i in range(j, len(M)):
        if M[i][j] != 0:
            return i

pivot(M, 1)

Question

En déduire une fonction descente(M) réalisant la descente du pivot de Gauss sur une matrice augmentée M, de façon à obtenir une matrice échelonnée (avec des 0 en dessous de la diagonale).
Il faut donc, pour chaque colonne \(j\) de M (sauf la dernière, qui correspond au second membre de la matrice augmentée):

Soit \(k\) le numéro de ligne renvoyé par pivot(M, j). Échanger la \(j\)ème ligne avec la \(k\)ème ligne de façon à ce que le coefficient \(m_{j, j}\) de M soit non nul.
Pour toute ligne \(i > j\), effectuer une transvection de façon à mettre un 0 sur la ligne \(i\), colonne \(j\) de M.

Solution

def descente(M):
    for j in range(len(M[0]) - 1):
        echange(M, j, pivot(M, j))
        for i in range(j+1, len(M)):
            transvection(M, i, j, -M[i][j]/M[j][j])

descente(M)
M

array([[ -4. ,   8. ,   2. , -36. ],
       [  0. ,  18. ,   3. , -66. ],
       [  0. ,   0. ,   2.5,  20. ]])

Question

De façon similaire, écrire une fonction remontee(M) parcourant les colonnes de M de droite à gauche (sauf la dernière) en mettant des 0 au dessus de la diagonale. On supposera dans cette fonction que tous les coefficients diagonaux sont non nuls: il n’y a donc pas besoin d’appeller pivot.

Solution

def remontee(M):
    for j in range(len(M[0]) - 2, -1, -1):
        for i in range(0, j):
            transvection(M, i, j, -M[i][j]/M[j][j])

remontee(M)
M

array([[ -4. ,   0. ,   0. , -12. ],
       [  0. ,  18. ,   0. , -90. ],
       [  0. ,   0. ,   2.5,  20. ]])

Question

Écrire une fonction gauss(M) prenant en argument une matrice augmentée M d’un système \(AX = B\) (c’est à dire M = (\(A \vert B\))) et appliquant la méthode du pivot de Gauss sur M. Pour cela, il faut :

Appliquer la fonction descente(M) sur M.
Appliquer la fonction remontee(M) sur M.
Mettre des \(1\) sur la diagonale de M avec des dilatations.
La solution du système \(AX = B\) est alors donnée par la dernière colonne de M.

Solution

def gauss(M):
    descente(M)
    remontee(M)
    for i in range(len(M)):
        dilatation(M, i, 1/M[i, i])

M1 = np.array([[-2.0,4.0,1.0,-18.0],[8.0,2.0,-1.0,6.0],[2.0,-1.0,2.0,27.0]])
gauss(M1)
M1 # la solution est sur la dernière colonne

array([[ 1., -0., -0.,  3.],
       [ 0.,  1.,  0., -5.],
       [ 0.,  0.,  1.,  8.]])

Informatique en 2ème année de BCPST

TP 6 : Application aux mathématiques

Contents

TP 6 : Application aux mathématiques#

Nombres complexes#

Vecteurs#

Polynômes#

Intégrale#

Méthode du pivot de Gauss#