TP 9 : Manipulation d’images
Contents
TP 9 : Manipulation d’images#

Rappels sur numpy#
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams["figure.figsize"] = (20,8) # modifie la taille des figures
On peut créer une matrice de taille \(n\times p\) remplie de \(0\) avec np.zeros((n,p)) :
m = np.zeros((2, 4))
m
array([[0., 0., 0., 0.],
[0., 0., 0., 0.]])
On peut accéder et modifier l’élément sur la ligne \(i\), colonne \(j\) avec m[i][j] :
m[0][0] = 1 # modifie l'élément ligne 0, colonne 0 (en haut à gauche)
m
array([[1., 0., 0., 0.],
[0., 0., 0., 0.]])
Exercice
Écrire une fonction identite telle que identite(n) renvoie une matrice identité de taille \(n\times n\).
Solution
def identite(n):
I = np.zeros((n, n))
for i in range(n):
I[i][i] = 1
return I
identite(5)
array([[1., 0., 0., 0., 0.],
[0., 1., 0., 0., 0.],
[0., 0., 1., 0., 0.],
[0., 0., 0., 1., 0.],
[0., 0., 0., 0., 1.]])
Si m est une matrice, len(m) est son nombre de lignes et len(m[0]) est son nombre de colonnes :
print(len(m)) # nombre de lignes
print(len(m[0])) # nombre de colonnes
2
4
On peut aussi utiliser m.shape pour obtenir les dimensions de la matrice (sous forme de tuple) :
m.shape # m est de dimension 2x4
(2, 4)
On peut parcourir une matrice avec deux boucles for (une boucle pour chaque indice) :
for i in range(len(m)): # parcourt les lignes
for j in range(len(m[0])): # parcourt les colonnes
m[i][j] = i + j # modifie la matrice
m
array([[0., 1., 2., 3.],
[1., 2., 3., 4.]])
Exercice
Écrire une fonction trace pour calculer la trace d’une matrice, c’est-à-dire la somme des éléments sur la diagonale.
Solution
def trace(m):
s = 0
for i in range(len(m)):
for j in range(len(m[0])):
s += m[i][j]
return s
trace(identite(5))
5.0
Il est possible d’effectuer une opération (+, *…) directement sur deux matrices (ou une matrice et un scalaire) :
m1 = np.array([[7, 2, 5], [1, 5, 6]]) # définition d'une matrice
m2 = np.array([[7, 0, 1], [6, 11, 12]]) # définition d'une autre matrice
m1 + m2 # addition de deux matrices
array([[14, 2, 6],
[ 7, 16, 18]])
Dans l’exemple ci-dessus, on a effectué l’opération : \(\begin{pmatrix} 7& 2& 5 \\ 1 & 5 & 6 \end{pmatrix} + \begin{pmatrix} 7 & 0 & 1 \\ 6 & 11 & 12 \end{pmatrix} = \begin{pmatrix} 14 & 2 &6 \\ 7 & 16 & 18 \end{pmatrix}\)
Images#
Une image est constituée d’un rectangle de pixels, chaque pixel ayant une couleur uniforme représentée par un nombre entier.
En Python, on utilise généralement un tableau numpy à \(3\) dimensions pour stocker une image.
m = plt.imread("lyon.jpg") # m est un tableau numpy contenant les pixels de l'image
m = m.astype(int)
plt.imshow(m) # afficher une image
plt.show()

m.shape # taille de l'image
(353, 550, 3)
La ligne précédente montre que m est de taille \(353 \times 550 \times 3\), ce qui signifie que l’image fait \(353\) pixels de hauteur, \(550\) pixels de largeur et que chaque pixel possède 3 niveaux de couleurs (rouge, vert et bleu, ou RGB), un niveau de couleur étant un nombre entier compris entre 0 (absence de couleur) et 255 (couleur complètement présente).
Par exemple, un pixel avec des niveaux RGB de \((255, 0, 0)\) est complètement rouge. Un pixel avec des niveaux RGB de \((255, 255, 0)\) est un mélange de rouge et de vert, c’est-à-dire du jaune.
On accède à un pixel avec m[i][j] :
m[12][263] # pixel sur la ligne 12, colonne 263
array([103, 149, 172])
Ainsi, le pixel sur la ligne \(12\), colonne \(263\), possède des valeurs RGB égales à \((103, 149, 172)\). Le pixel de coordonnées \((0, 0)\) est celui en haut à gauche. Mettons du rouge sur un carré \(100\times 100\) en haut à gauche :
m_red = m.copy()
for i in range(100):
for j in range(100):
m_red[i][j] = np.array([255, 0, 0]) # on met tous les pixels en rouge
plt.imshow(m_red)
plt.show()

Exercice
Modifier le code précédent de façon à cacher la tour Part-Dieu (“tour crayon”), en mettant un rectangle bleu dessus.
Solution
m_red = m.copy()
for i in range(0, 100):
for j in range(250, 300):
m_red[i][j] = np.array([0, 0, 255]) # on tous les pixels en rouge
plt.imshow(m_red)
plt.show()
<Figure size 2000x800 with 1 Axes>
Inversion des couleurs#
On peut inverser les couleurs d’une images en remplaçant chaque m[i][j] par 255 - m[i][j].
Exercice
Inverser les couleurs d’une image pour obtenir l’image ci-dessous. On pourra compléter le code suivant (dont on pourra aussi s’inspirer pour toutes les questions suivantes).
def inverse(m):
m = m.copy() # pour éviter de modifier la matrice en dehors de la fonction
... # parcourir m[i][j] en remplacant par 255 - m[i][j]
return m
Solution
def inverse(m):
m = m.copy() # pour éviter de modifier la matrice en dehors de la fonction
for i in range(len(m)):
for j in range(len(m[0])):
m[i][j] = 255 - m[i][j]
return m
plt.imshow(inverse(m))
plt.show()

Rotation#
Faire une rotation sur l’image revient à prendre la matrice transposée : il faut inverser ligne et colonne. Si m est de taille \(n\times p \times 3\), il faut donc créer une matrice m2 de taille \(p\times n\times 3\) telle que m2[i][j] = m[j][i].
Exercice
Écrire une fonction rotation(m) renvoie une matrice correspondant à la rotation de m. Il faut commencer par créer une nouvelle matrice avec np.zeros((..., ..., 3), dtype=int) avec les bonnes dimensions.
Solution
def rotation(m):
res = np.zeros((len(m[0]), len(m), 3), dtype=int)
for i in range(len(m)):
for j in range(len(m[0])):
res[j][i] = m[i][j]
return res
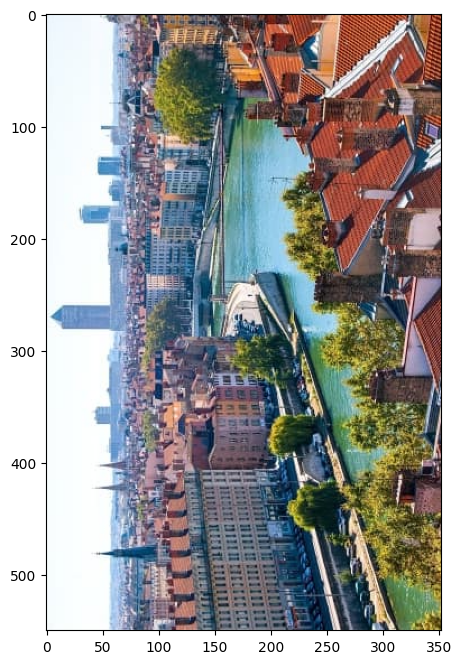
plt.imshow(rotation(m))
plt.show()
Niveaux de gris#
On peut transformer une image couleur en une image en niveaux de gris en remplaçant chaque pixel par la moyenne de ses trois couleurs.
Question
Écrire une fonction niveau_gris(m) qui renvoie une matrice correspondant à l’image en niveaux de gris de m. On pourra compléter le code ci-dessous.
def niveau_gris(m):
m2 = np.zeros((len(m), len(m[0])), dtype=int) # matrice de même taille que m, mais avec qu'un seul niveau de couleur
for i in range(len(m)):
for j in range(len(m[0])):
... # remplacer m2[i][j] par la moyenne des trois niveaux de couleur de m[i][j]
return m2
Solution
def niveau_gris(m):
res = np.zeros((len(m), len(m[0])), dtype=int)
for i in range(len(m)):
for j in range(len(m[0])):
res[i][j] = int(np.mean(m[i][j]))
return res
plt.imshow(niveau_gris(m), cmap="gray")
plt.show()

Redimensionnement#
On peut réduire la taille d’une image en divisant sa largeur et sa hauteur par un facteur \(k\). Il faut donc définir une matrice m2 de taille \((n/k)\times (p/k)\times 3\) telle que m2[i][j] = m[i*k][j*k].
Exercice
Écrire une fonction reduction(m, k) renvoie une matrice correspondant au réduction de m par un facteur k.
Solution
def reduction(m, k): # divise largeur et hauteur par k
m_red = np.zeros((len(m)//k, len(m[0])//k, 3), dtype=np.uint8) # matrice de taille divisée par k
for i in range(len(m_red)):
for j in range(len(m_red[0])):
m_red[i][j] = m[i*k][j*k]
return m_red
plt.imshow(reduction(m, 3))
plt.show()

Exercice
Faire de même pour augmenter la résolution de l’image. Il faut inverser // et * par rapport à la fonction précédente.
Solution
def augmentation(m, k): # remarque : on pourrait juste appliquer la fonction précédente avec 1/k...
m_red = np.zeros((len(m)*k, len(m[0])*k, 3), dtype=np.uint8) # matrice de taille divisée par k
for i in range(len(m_red)):
for j in range(len(m_red[0])):
m_red[i][j] = m[i//k][j//k]
return m_red
plt.imshow(augmentation(m, 2))
plt.show()

Convolution#
Flou#
En modifiant chaque pixel par la moyenne des (au plus) 9 pixels adjacents, on peut faire un effet de flou. Il faut cependant faire attention à ne pas dépasser les bords de l’image.
Exercice
Écrire une fonction moyenne telle que, si m est une matrice, moyenne(m, i, j) renvoie la moyenne des \(9\) pixels adjacents autour de m[i][j] (c’est-à-dire de m[i+1][j], m[i-1][j]…), sans prendre en compte les pixels sortants de l’image.
Solution
def moyenne(m, i, j):
n = 0
moy = 0
for k in [i - 1, i, i + 1]:
for l in [j - 1, j, j + 1]:
if -1 < k < len(m) and -1 < l < len(m[0]):
moy += m[k][l]
n += 1
return moy/n
moyenne(m, 0, 0)
array([242.25, 251.25, 254.75])
Exercice
En déduire une fonction flou telle que flou(m) renvoie une image obtenue en prenant la moyenne de chaque pixel dans m. Essayer d’appliquer plusieurs fois flou.
Solution
def flou(m):
m_flou = m.copy()
for i in range(len(m)):
for j in range(len(m[0])):
m_flou[i][j] = (moyenne(m, i, j))
return m_flou
plt.imshow(flou(m))
plt.show()

Détection de contours#
Plutôt que de faire la moyenne des pixels adjacents, on peut faire une moyenne pondérée. Par exemple, pour détecter les contours dans une image, on peut donner un poids de \(8\) au pixel central et un poids de \(-1\) aux pixels adjacents, ce qui correspond au filtre laplacien suivant :
Si \(M = (m_{i, j})\), il faut donc calculer la matrice \(M' = (m_{i, j}')\) telle que :
Sachant qu’on ne prend pas en compte les pixels en dehors de l’image.
Question
Écrire une fonction detection_contours(m) qui renvoie la matrice m2 telle que m2[i][j] est la moyenne pondérée des pixels adjacents à m[i][j].
Solution
def detection_contours(m):
m_contours = m.copy()
for i in range(len(m)):
for j in range(len(m[0])):
m_contours[i][j] = 9*m[i][j] - 9*moyenne(m, i, j)
return m_contours
plt.imshow(detection_contours(m))
plt.show()
Clipping input data to the valid range for imshow with RGB data ([0..1] for floats or [0..255] for integers).

Le filtre de Sobel est un autre filtre, permettant spécifiquement de détecter les contours horizontaux et verticaux. Pour détecter un contours vertical, il est défini par :
Question
Écrire une fonction sobel(m) faisant la même chose que detection_contours, mais avec le filtre de Sobel ci-dessus.
Solution
def sobel(m):
m_sobel = np.zeros_like(m)
for i in range(len(m)):
for j in range(len(m[0])):
if i >= 1:
m_sobel[i][j] -= 2*m[i - 1][j]
if i >= 1 and j >= 1:
m_sobel[i][j] -= m[i - 1][j - 1]
if i >= 1 and j < len(m[0]) - 1:
m_sobel[i][j] -= m[i - 1][j + 1]
if i < len(m) - 1:
m_sobel[i][j] += 2*m[i + 1][j]
if i < len(m) - 1 and j >= 1:
m_sobel[i][j] += m[i + 1][j - 1]
if i < len(m) - 1 and j < len(m[0]) - 1:
m_sobel[i][j] += m[i + 1][j + 1]
return m_sobel
plt.imshow(sobel(niveau_gris(m)), cmap="gray")
plt.show()



