TP 18 : Révisions graphes

Graphes

Un graphe est un ensemble de sommets (ronds) reliés par des arêtes (traits).
Deux sommets sont voisins s’ils sont reliés par une arête.

Un graphe peut être représenté par une matrice d’adjacence \(A = (a_{i, j})\) de taille \(n \times n\) où \(n\) est le nombre de sommets, où \(a_{i, j} = 1\) si les sommets \(i\) et \(j\) sont voisins et \(a_{i, j} = 0\) sinon.

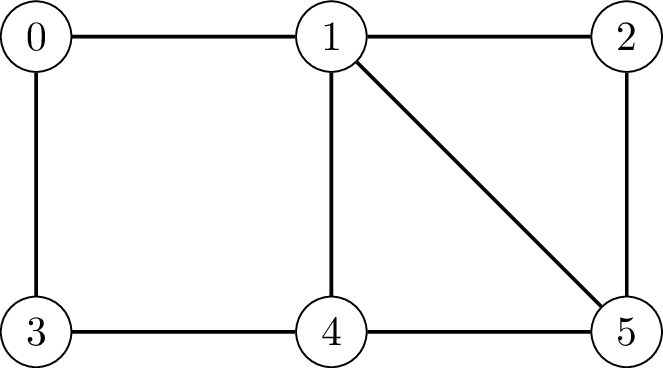
Question

Définir le graphe ci-dessus dans une matrice \(A\).

Solution

A =  [
    [0, 1, 0, 1, 0, 0],
    [1, 0, 1, 0, 1, 1],
    [0, 1, 0, 0, 0, 1],
    [1, 0, 0, 0, 1, 0],
    [0, 1, 0, 1, 0, 1],
    [0, 1, 1, 0, 1, 0]
]

Question

Écrire une fonction voisins(A, v) renvoyant la liste des voisins du sommet \(v\) dans le graphe \(A\).

Solution

def voisins(A, v):
    L = []
    for i in range(len(A[0])):
        if A[v][i] == 1:
            L.append(i)
    return L

voisins(A, 1)

[0, 2, 4, 5]

Question

Le degré d’un sommet est son nombre de voisins. Écrire une fonction degre(A, v) renvoyant le degré de v.

Solution

def degre(A, v):
    return len(voisins(A, v))

degre(A, 1)

4

Question

Écrire une fonction nombre_arete(A) renvoyant le nombre d’arêtes du graphe \(A\).

Solution

def nombre_arete(A):
    n = 0
    for v in range(len(A)):
        n += degre(A, v)
    return n//2

nombre_arete(A)

8

Un graphe est complet s’il contient toutes les arêtes possibles.

Exemple de graphe complet

Question

Écrire une fonction complet(n) renvoyant la matrice d’adjacence du graphe complet à \(n\) sommets.

Solution

def complet(n):
    M = []
    for i in range(n):
        L = []
        for j in range(n):
            L.append(1)
        M.append(L)
    for i in range(n):
        M[i][i] = 0
    return M

complet(5)

[[0, 1, 1, 1, 1],
 [1, 0, 1, 1, 1],
 [1, 1, 0, 1, 1],
 [1, 1, 1, 0, 1],
 [1, 1, 1, 1, 0]]

Question

Écrire une fonction est_complet(A) renvoyant True si le graphe \(A\) est complet et False sinon.

Solution

def est_complet(A):
    n = len(A)
    for i in range(n):
        for j in range(n):
            if i != j and A[i][j] == 0:
                return False
    return True

print(est_complet(A))
print(est_complet(complet(5)))

False
True