TP 10 : Automates cellulaires
Contents
TP 10 : Automates cellulaires#
Un automate cellulaire consiste en une grille (matrice) de cellules contenant chacune un état qui peut évoluer au cours du temps. L’état d’une cellule au temps \(t+1\) dépend de l’état au temps \(t\) des cellules adjacentes.
Rappels sur numpy#
import numpy as np
On peut créer une matrice de taille \(n\times p\) remplie de \(0\) avec np.zeros((n,p)) :
m = np.zeros((2, 4))
m
array([[0., 0., 0., 0.],
[0., 0., 0., 0.]])
On peut accéder et modifier l’élément sur la ligne \(i\), colonne \(j\) avec m[i][j] :
m[0][0] = 1 # modifie l'élément ligne 0, colonne 0 (en haut à gauche)
m
array([[1., 0., 0., 0.],
[0., 0., 0., 0.]])
Exercice
Écrire une fonction identite telle que identite(n) renvoie une matrice identité de taille \(n\times n\).
Solution
def identite(n):
I = np.zeros((n, n))
for i in range(n):
I[i][i] = 1
return I
identite(5)
array([[1., 0., 0., 0., 0.],
[0., 1., 0., 0., 0.],
[0., 0., 1., 0., 0.],
[0., 0., 0., 1., 0.],
[0., 0., 0., 0., 1.]])
Si m est une matrice, len(m) est son nombre de lignes et len(m[0]) est son nombre de colonnes :
print(len(m)) # nombre de lignes
print(len(m[0])) # nombre de colonnes
2
4
On peut aussi utiliser m.shape pour obtenir les dimensions de la matrice (sous forme de tuple) :
m.shape # m est de dimension 2x4
(2, 4)
On peut parcourir une matrice avec deux boucles for (une boucle pour chaque indice) :
for i in range(len(m)): # parcourt les lignes
for j in range(len(m[0])): # parcourt les colonnes
m[i][j] = i + j # modifie la matrice
m
array([[0., 1., 2., 3.],
[1., 2., 3., 4.]])
Exercice
Écrire une fonction trace pour calculer la trace d’une matrice, c’est-à-dire la somme des éléments sur la diagonale.
Solution
def trace(m):
s = 0
for i in range(len(m)):
for j in range(len(m[0])):
s += m[i][j]
return s
trace(identite(5))
5.0
Fonctions utilitaires#
Si m est une matrice, len(m) est son nombre de lignes et len(m[0]) est son nombre de colonnes :
Question
Écrire une fonction bernouilli(p) renvoyant \(1\) avec une probabilité \(p\) et \(0\) avec une probabilité \(1 - p\).
On utilisera np.random.rand() pour générer un nombre aléatoire entre 0 et 1
Solution
def bernouilli(p):
if np.random.rand() < p:
return 1
return 0
Question
Écrire une fonction compter(L, e) qui renvoie le nombre d’occurrences de l’élément e dans la liste L.
Solution
def compter(L, e):
n = 0
for x in L:
if x == e:
n += 1
return n
compter([1, 0, 1, 1, 0, 0, 1], 1)
4
Question
Écrire une fonction matrice_aleatoire(n, p) qui renvoie une matrice de taille \(n \times n\) dont chaque élément est égal à 1 avec une probabilité \(p\) et 0 sinon.
On utilisera np.zeros((n, n), dtype=int) pour créer une matrice de taille \(n \times n\) remplie de 0.
Solution
def matrice_aleatoire(n, p):
M = np.zeros((n, n), dtype=int)
for i in range(n):
for j in range(n):
if bernouilli(p):
M[i, j] = 1
return M
M = matrice_aleatoire(5, 0.2)
M
array([[0, 0, 1, 1, 1],
[1, 0, 0, 1, 0],
[0, 1, 1, 0, 0],
[1, 0, 1, 1, 0],
[0, 0, 0, 0, 0]])
Question
Écrire une fonction voisins(M, i, j) qui renvoie la liste des \(8\) voisins de la case (i, j) de la matrice M. Il s’agit donc des valeurs en position \((k, l)\) où \(k \in \{i-1, i, i+1\}\), \(l \in \{j-1, j, j+1\}\) et \((k, l) \neq (i, j)\). On fera attention à ne pas dépasser de la matrice.
Solution
def voisins(A, i, j) :
n, p = A.shape
L = []
for k in range(i-1, i+2) :
for l in range(j-1, j+2) :
if 0 <= k < n and 0 <= l < p and (k != i or l != j):
L.append(A[k, l])
return L
voisins(M, 3, 1)
[0, 1, 1, 1, 1, 0, 0, 0]
Jeu de la vie#
Le jeu de la vie a été inventé par le mathématicien John Conway en 1970, et peut être vu comme la modélisation d’une population de cellules biologiques.
À chaque étape, une cellule peut être en vie (\(1\)) ou morte (\(0\)), avec les règles suivantes :
Une cellule morte possédant exactement trois cellules voisines vivantes devient vivante (elle naît).
Une cellule vivante possédant deux ou trois cellules voisines vivantes le reste, sinon elle meurt.
Question
Écrire une fonction regle_jeu_vie(M, i, j) qui renvoie l’état de la cellule (i, j) à l’étape suivante. On pourra réutiliser les fonctions voisins et compter écrites précédemment.
Solution
def regle_jeu_vie(A, i, j):
n = compter(voisins(A, i, j), 1)
if A[i, j] == 1:
if n == 2 or n == 3:
return 1
return 0
if n == 3:
return 1
return 0
print(regle_jeu_vie(M, 3, 1))
print(regle_jeu_vie(M, 2, 2))
0
0
Question
Écrire une fonction etape_jeu_vie(M) qui renvoie la matrice correspondant à l’étape suivante du jeu de la vie.
Attention : il ne faut pas modifier M, mais renvoyer une nouvelle matrice.
Solution
def etape_jeu_vie(M):
n, p = M.shape
B = np.zeros((n, p), dtype=int)
for i in range(n):
for j in range(p):
B[i, j] = regle_jeu_vie(M, i, j)
return B
Question
Utiliser la fonction jeu_vie ci-dessous pour afficher l’évolution du jeu de la vie, en utilisant sa documentation.
Remarque : si vous avez des problèmes après avoir fermé la fenêtre graphique, cliquer sur le bouton “Arrêter l’exécution” (en haut à droite dans Pyzo).
import matplotlib as mpl
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
from IPython.display import HTML
def jeu_vie(M, n):
"""Affiche les n premières étapes du jeu de la vie.
M : matrice initiale
etape_jeu_vie : fonction qui calcule l'étape suivante
n : nombre d'étapes
"""
fig = plt.figure()
def update(i) :
nonlocal M
plt.imshow(M, interpolation='nearest', origin='lower', cmap="gray")
plt.title(f"Itération {i}")
if i != 0:
M = etape_jeu_vie(M)
plt.axis('off')
anim = FuncAnimation(fig, update, frames=n, interval=300, repeat=False)
plt.show()
# return HTML(anim.to_jshtml())
jeu_vie(matrice_aleatoire(20, 0.5), 30)

Feu de forêt#
Nous souhaitons ici modéliser un feu de forêt. Chaque case de la matrice correspondra à un arbre qui peut prendre l’une des valeurs suivantes :
\(0\) : arbre non brûlé.
\(-1\) : arbre complètement brûlé.
un entier \(t \in \mathbb{N}^*\) : arbre en train de brûler, où \(t\) est le nombre d’étapes restantes avant que l’arbre ne soit complètement brûlé.
Question
Écrire une fonction voisin_brule(M, i, j) qui renvoie True si la case (i, j) de la matrice M est adjacente à au moins une case contenant un arbre en train de brûler et False sinon.
Solution
def voisin_brule(A, i, j) :
L = voisins(A, i, j)
for e in L:
if e > 0:
return True
return False
À chaque étape :
Une case contenant un entier \(t > 1\) devient \(t-1\) (arbre en train de brûler).
Une case contenant \(1\) devient \(-1\) (arbre complètement brûlé).
Une case contenant \(0\) qui est adjacente à au moins une case contenant \(1\) devient \(3\) avec une probabilité \(p\) (un arbre qui prend feu brûle pendant \(3\) tours). Sinon, cette case reste à \(0\).
Question
Écrire une fonction regle_feu(M, i, j, p) qui renvoie l’état de la case (i, j) à l’étape suivante, où p est la probabilité ci-dessus.
Solution
def regle_feu(M, i, j, p):
e = M[i, j]
if e > 1:
return e - 1
if e == 1 or e == -1:
return -1
if voisin_brule(M, i, j) and bernouilli(p) == 1:
return 3
return 0
Question
Écrire une fonction etape_feu(M, p) qui renvoie la matrice correspondant à l’étape suivante du feu de forêt. Attention : il ne faut pas modifier M, mais renvoyer une nouvelle matrice.
Solution
def etape_feu(M, p):
n = len(M)
B = np.zeros((n, n), dtype=int)
for i in range(n):
for j in range(n):
B[i, j] = regle_feu(M, i, j, p)
return B
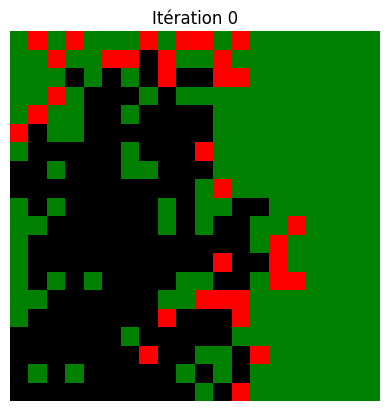
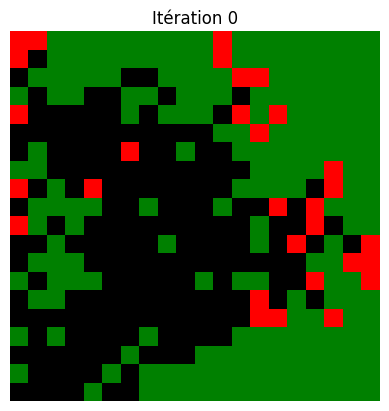
Question
Utiliser la fonction feu_foret ci-dessous pour afficher l’évolution d’un feu de forêt, en utilisant sa documentation. Tester avec différentes probabilités de propagation du feu, en changeant la position du premier arbre en feu…
def feu_foret(M, n, p):
"""Affiche les n premières étapes du jeu de la vie.
M : matrice initiale
etape_jeu_vie : fonction qui calcule l'étape suivante
n : nombre d'étapes
"""
fig = mpl.pyplot.figure()
cmap = mpl.colors.ListedColormap(['black', 'green', 'red'])
bounds = [-1,-0.5, 0.5, 1]
norm = mpl.colors.BoundaryNorm(bounds, cmap.N)
def update (i) :
nonlocal M
mpl.pyplot.imshow(M, interpolation='nearest', origin='lower', cmap=cmap, norm=norm)
mpl.pyplot.title(f"Itération {i}")
if i != 0:
M = etape_feu(M, p)
mpl.pyplot.axis('off')
anim = FuncAnimation(fig, update, frames=n, interval=300, repeat=False)
plt.show()
#return HTML(anim.to_jshtml())
M = np.zeros((20, 20), dtype=int)
M[5][5] = 3 # un arbre en feu initialement
feu_foret(M, 30, 0.15)