TP 19 : Simulation de collision

Particules dans une boîte

On considère des particules sous forme de disque, définies par le type ci-dessous.

from dataclasses import dataclass

@dataclass
class Particule:
    x: float
    y: float
    vx: float
    vy: float
    m: float
    r: float

Vous n’avez pas besoin de comprendre le code ci-dessus, mais seulement de savoir l’utiliser :

p = Particule(x=0, y=0, vx=1, vy=1, m=1, r=1) # pour définir une particule
print(p.x) # accéder à la position suivant x
print(p.vx) # accéder à la vitesse suivant x
p.vx = 2 # modifier la vitesse suivant x

0
1

Question

Écrire une fonction aleatoire(a, b) qui renvoie un nombre aléatoire dans l’intervalle \([a, b]\). Pour cela on utilisera random() de la bibliothèque random, qui renvoie un nombre aléatoire dans l’intervalle \([0, 1]\).

aleatoire(1, 10)

6.124254375168906

Question

Écrire une fonction particules_aléatoires(n) qui renvoie une liste de n particules aléatoires p où :

• p.x et p.y sont des coordonnées aléatoires dans l’intervalle \([0, 10]\).

• p.vx et p.vy sont des vitesses aléatoires dans l’intervalle \([-1, 1]\).

• p.m est une masse aléatoire dans l’intervalle \([1, 10]\).

• p.r est égal à \(0.5\).

On utilisera random() du module random pour générer un nombre aléatoire dans l’intervalle \([0, 1]\).

particules_aléatoires(3)

[Particule(x=5.223220080376285, y=8.920130314606784, vx=0.05022210059556098, vy=-0.8512038349545941, m=2.264370339299915, r=0.5),
 Particule(x=1.9763078437953852, y=0.4281365850796104, vx=0.8034415893697311, vy=0.8271995031459225, m=2.964015402614194, r=0.5),
 Particule(x=2.4682814501937744, y=8.037961568338547, vx=0.13827098423564177, vy=0.8514548612044701, m=6.943890305958839, r=0.5)]

Question

Écrire une fonction avance(p, dt) qui déplace la position de la particule p pendant dt secondes.
Il faut donc modifier p.x et p.y en fonction de p.vx, p.vy et dt.

p = Particule(x=0, y=0, vx=1, vy=2, m=1, r=1)
avance(p, .1)
p

Particule(x=0.1, y=0.2, vx=1, vy=2, m=1, r=1)

On suppose que la particule p est dans un carré de hauteur et largeur \(h\).
Si p touche un bord vertical du carré, on change le signe de p.vx (p.vx = -p.vx).
Si p touche un bord horizontal du carré, on change le signe de p.vy.

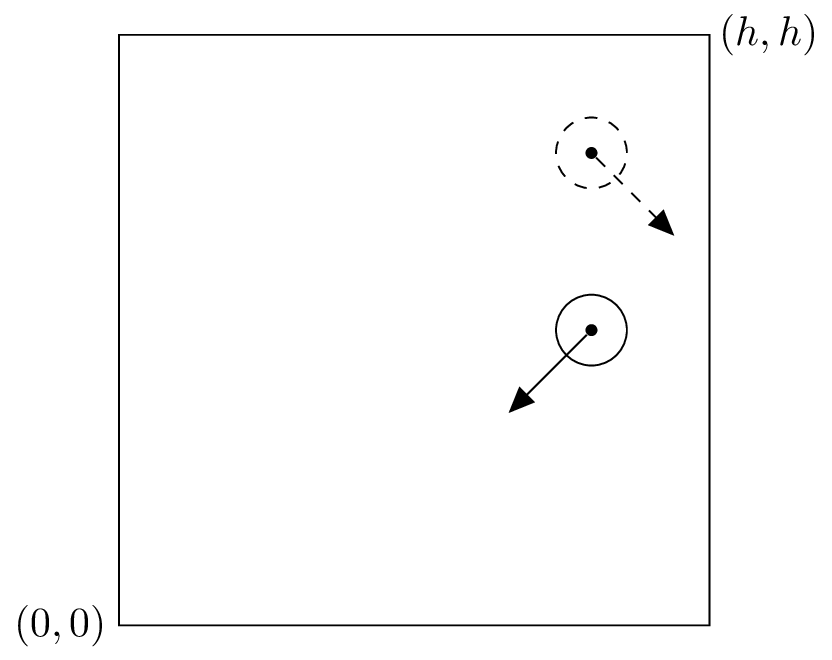
Particule avant et après collision avec un bord

Question

Écrire une fonction bord(p, h) qui modifie la vitesse de p si elle touche un bord du carré.

Question

Écrire une fonction etape(particules, h, dt) qui parcourt chaque particule p de la liste particules et qui appelle bord et avance dessus.
Tester avec animation(particules_aléatoires(3)) (on pourra changer le nombre de particules).

import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
from IPython.display import HTML
from matplotlib.patches import Circle

def animation(particules, n=200):
    h = 10
    fig = plt.figure()
    ax = plt.axes(xlim=(0, h), ylim=(0, h))
    ax.set_aspect('equal', 'box')
    cercles = [Circle(xy=(p.x, p.y), radius=p.r) for p in particules]
    for c in cercles:
        ax.add_patch(c)
    def init():
        return cercles
    def animate(i):
        for _ in range(30):
            etape(particules, h, .01)
        for c, p in zip(cercles, particules):
            c.center = (p.x, p.y)
        return cercles
    anim = FuncAnimation(fig, animate, init_func=init, frames=n, interval=20, blit=True)
    plt.show()
    # return HTML(anim.to_jshtml())

animation(particules_aléatoires(3))

Once Loop Reflect

Collisions entre particules

On considère deux particules p1 et p2 et on veut savoir si elles se touchent.

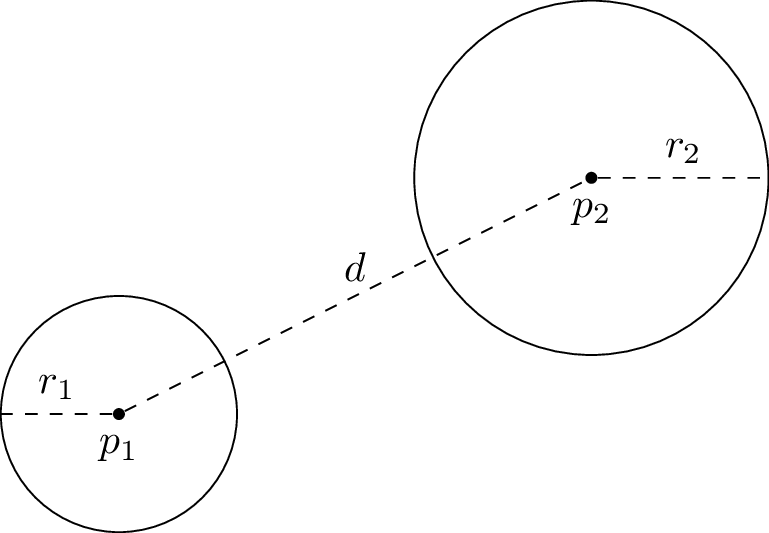
Question

Sur la figure ci-dessus, à quelle condition sur \(d\), \(r_1\), \(r_2\) y a t-il collision entre \(p_1\) et \(p_2\) ?
En déduire une fonction collision(p1, p2) qui prend en argument deux particules et qui renvoie True si elles sont en collision et False sinon.

print(collision(Particule(x=0, y=0, vx=1, vy=2, m=1, r=1), Particule(x=.5, y=.5, vx=1, vy=2, m=1, r=1)))
print(collision(Particule(x=0, y=0, vx=1, vy=2, m=1, r=1), Particule(x=2, y=2, vx=1, vy=2, m=1, r=1)))

True
False

En une dimension

On considère une collision parfaitement élastique (c’est-à-dire que l’énergie cinétique \(\frac{1}{2}mv^2\) et la quantité de mouvement \(mv\) sont conservées) entre deux particules \(p_1\) et \(p_2\), le long d’un axe \(x\).

On appelle \(v_1\) la vitesse de \(p_1\) avant le choc et \(v_1'\) la vitesse après le choc. De même pour \(p_2\).

Question

Écrire les équations obtenues par conservation de l’énergie cinétique et de la quantité de mouvement.

Question

En déduire une expression pour \(v_1'\) et \(v_2'\).

Question

Écrire une fonction vitesse_collision(p1, p2) qui modifie p1.vx et p2.vx en v1' et v2'.

Question

Réécrire la fonction etape(particules, h, dt) en appelant collision et vitesse_collision pour simuler les collisions parmis les particules.

Question

Tester avec l’appel de fonction ci-dessous. On pourra changer les masses, les vitesses et rajouter des particules.

animation([Particule(x=3, y=5, vx=2, vy=0, m=1, r=.5), Particule(x=6, y=5, vx=0, vy=0, m=10, r=.5)])

Once Loop Reflect

En deux dimensions

On note \(\mathbf{c}_1\), \(\mathbf{v}_1\) le vecteur position et le vecteur vitesse de \(p_1\). De même pour \(p_2\).
On peut alors montrer que les vecteurs vitesses après collision (en deux dimensions) sont donnés par :

(1)\[\begin{align} \mathbf{v}'_1&=\mathbf{v}_1-\frac{2 m_2}{m_1+m_2} \ \frac{\langle \mathbf{v}_1-\mathbf{v}_2,\,\mathbf{c}_1-\mathbf{c}_2\rangle}{\|\mathbf{c}_1-\mathbf{c}_2\|^2} \ (\mathbf{c}_1-\mathbf{c}_2), \\ \mathbf{v}'_2&=\mathbf{v}_2-\frac{2 m_1}{m_1+m_2} \ \frac{\langle \mathbf{v}_2-\mathbf{v}_1,\,\mathbf{c}_2-\mathbf{c}_1\rangle}{\|\mathbf{c}_2-\mathbf{c}_1\|^2} \ (\mathbf{c}_2-\mathbf{c}_1) \end{align}\]

Les opérations ci-dessus étant vectorielles, il est plus pratique d’utiliser numpy, pour additioner et multiplier des vecteurs :

import numpy as np

p1, p2 = Particule(x=0, y=0, vx=1, vy=2, m=1, r=1), Particule(x=2, y=2, vx=1, vy=2, m=1, r=1) # exemple
v1, v2 = np.array([p1.vx, p1.vy]), np.array([p2.vx, p2.vy])
print(v1 + v2) # addition de vecteurs
print(np.dot(v1, v2)) # produit scalaire
print(np.dot(v1, v1)) # norme de v1 (produit scalaire de v1 et v1)

[2 4]
5

Question

Réécrire vitesse_collision(p1, p2) en utilisant numpy et les équations ci-dessus. Tester avec animation(particules_aléatoires(5)).

animation(particules_aléatoires(5))

Once Loop Reflect

Avec la gravité

Question

Réécrire avance(p, dt) en ajoutant la gravité. Exceptionnellement, on prendra \(g = 0.4\).

animation(particules_aléatoires(3))

Once Loop Reflect