DM : Redimensionnement d’image par Seam Carving

---

Ce DM est à effectuer sur Capytale (cliquer ici). Il faut se connecter avec ” Ma Classe en Région (Auvergne-Rhône-Alpes)” en utilisant ses identifiants ENT. Si vous n’avez pas vos identifiants ENT, vous pouvez utiliser Basthon en téléchargeant l’image (ici) puis en la chargeant sur Basthon avec Fichier -> Ouvrir…

---

L’objectif est de redimensionner une image par la méthode de Seam Carving. Cette technique consiste à supprimer des chemins d’énergie minimale sur l’image, c’est-à-dire utilisant des pixels de couleurs relativement uniformes. Ainsi, on évite de trop modifier l’image.

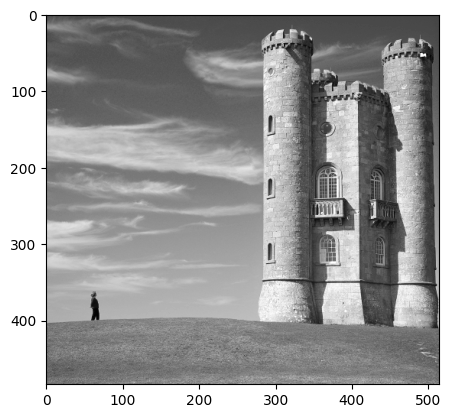
Image que l'on souhaite redimensionner

Redimensionnement classique, l'image est déformée.


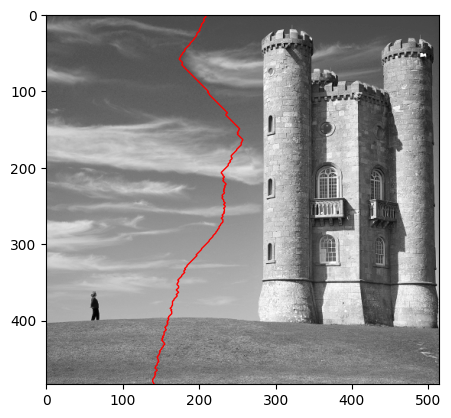
Redimensionnement par seam carving, un chemin d'énergie minimale étant représenté en rouge.

Chargement de l’image

Commençons par charger l’image :

import matplotlib.pyplot as plt
import numpy as np

m = plt.imread('tower.png')
plt.imshow(m, cmap='gray') # affiche l'image
plt.show()

La variable m que nous venons de définir contient alors une matrice numpy qui représente l’image. Comme l’image est en niveau de gris, chaque pixel est représenté par un nombre flottant (float) entre 0 (noir) et 1 (blanc).

print("valeur du pixel en haut à gauche :", m[0][0])
print("nombre de lignes :", len(m))
print("nombre de colonnes :", len(m[0]))
print("dimensions de l'image :", np.shape(m)) # une autre façon possible avec une matrice numpy

valeur du pixel en haut à gauche : 0.28627452
nombre de lignes : 484
nombre de colonnes : 714
dimensions de l'image : (484, 714)

Calcul de gradient

On définit une matrice \(g = (g_{i, j})\) de même dimension que \(m\) telle que :

\[g_{i, j} = |m_{i + 1, j} - m_{i - 1, j}| + |m_{i, j + 1} - m_{i, j - 1}|\]

La formule ci-dessus n’étant pas valable pour la première/dernière ligne (\(i = 0\) ou \(i = n - 1\), où \(n\) est le nombre de lignes de \(m\)), on utilise à la place :

\[g_{0, j} = |m_{1, j} - m_{0, j}| + |m_{i, j + 1} - m_{i, j - 1}|\]

\[g_{n - 1, j} = |m_{n - 1, j} - m_{n - 2, j}| + |m_{i, j + 1} - m_{i, j - 1}|\]

Et de même sur la première/dernière colonne.

Intuitivement, \(g_{i, j}\) correspond à l’intensité du gradient de l’image sur le pixel \(i, j\) : plus il est grand, plus il y a de fortes variation de couleur au niveau de ce pixel.

Question

Écrire une fonction matrice_gradient(m) qui renvoie g à partir de m. On pourra utiliser, au choix, une liste de listes ou un tableau numpy (en utilisant, par exemple, np.zeros((..., ...)) pour créer g). On pourra utiliser abs pour la valeur absolue.

Solution

def matrice_gradient(m):
    n, k = np.shape(m)
    g = np.zeros((n, k))
    g[0][0] = abs(m[1][0] - m[0][0]) + abs(m[0][1] - m[0][0])
    g[n-1][k-1] = abs(m[n-1][k-1] - m[n-2][k-1]) + abs(m[n-1][k-1] - m[n-1][k-2])
    g[0][k-1] = abs(m[1][k-1] - m[0][k-1]) + abs(m[0][k-1] - m[0][k-2])
    g[n-1][0] = abs(m[n-1][0] - m[n-2][0]) + abs(m[n-1][1] - m[n-1][0])
    for i in range(1, n-1):
        g[i][0] = abs(m[i+1][0] - m[i-1][0]) + abs(m[i][1] - m[i][0])
        g[i][k-1] = abs(m[i+1][k-1] - m[i-1][k-1]) + abs(m[i][k-1] - m[i][k-2])
    for j in range(1, k-1):
        g[0][j] = abs(m[1][j] - m[0][j]) + abs(m[0][j+1] - m[0][j-1])
        g[n-1][j] = abs(m[n-1][j] - m[n-2][j]) + abs(m[n-1][j+1] - m[n-1][j-1])
    for i in range(1, n-1):
        for j in range(1, k-1):
            g[i][j] = abs(m[i+1][j] - m[i-1][j]) + abs(m[i][j+1] - m[i][j-1])
    return g

g = matrice_gradient(m)
plt.imshow(g, cmap='gray') # affichage pour vérifier
plt.show()

Dans la suite, on pourra utiliser la fonction suivante qui sera plus rapide, a priori :

def matrice_gradient(m):
    g = np.zeros_like(m)
    g[1:-1] = np.abs(m[2:] - m[:-2])
    g[0] = np.abs(m[1] - m[0])
    g[-1] = np.abs(m[-1] - m[-2])
    g[:, 1:-1] += np.abs(m[:, 2:] - m[:, :-2])
    g[:, 0] += np.abs(m[:, 1] - m[:, 0])
    g[:, -1] += np.abs(m[:, -1] - m[:, -2])
    return g

Enlever un chemin

Nous enlèverons seulement des chemins verticaux. Un chemin sera donné par une liste c contenant les pixels m[i][c[i]]. Par exemple, si c = [231, 230, 231...] alors c passe par le pixel m[0][231], puis m[1][230], m[2][231]…

Question

Écrire une fonction enlever_chemin telle que, si m est une image de taille \(n\times p\), enlever_chemin(m, c) renvoie une matrice m2 de taille \(n\times (p - 1)\) obtenue à partir de m en supprimant chaque pixel du chemin c. On pourra compléter le code suivant :

def enlever_chemin(m, c):
    n, p = np.shape(m) # n est le nombre de lignes, p le nombre de colonnes
    m2 = [] # définition de m2 comme liste de listes
    for i in range(n):
        l = [] # ième ligne de m2
        for j in range(p):
            ... # ajouter la ligne m[i] sauf m[i][c[i]]
        ... # ajouter la ligne l à m2
    return np.array(m2) # conversion en matrice numpy

Solution

def enlever_chemin(m, c):
    n, p = np.shape(m)
    m2 = []
    for i in range(n):
        l = []
        for j in range(p):
            if j != c[i]:
                l.append(m[i][j])
        m2.append(l)
    return np.array(m2)

Calcul d’un chemin d’énergie minimum par programmation dynamique

On ne considère que les chemins verticaux.
L’énergie d’un chemin est définie comme la somme des gradients (\(g_{i, j}\)) des pixels du chemin.
Soit \(d_{i, j}\) l’énergie minimum d’un chemin depuis le haut de l’image jusqu’à un pixel \(i, j\).
Pour atteindre le pixel \(i, j\), on peut soit passer par le pixel \(i - 1, j - 1\), soit \(i - 1, j\) ou \(i - 1, j + 1\).
On a donc :

\[d_{i, j} = \min(d_{i - 1, j - 1}, d_{i - 1, j}, d_{i - 1, j + 1}) + g_{i, j}\]

\[d_{0, j} = g_{0, j}\]

Remarque : attention à ne pas dépasser les bords de l’image (on ne prend pas en compte le pixel \(i - 1, j - 1\) si \(j = 0\), par exemple).

Question

Écrire une fonction dp_chemin(g) qui renvoie une matrice d de même dimension que g telle que d[i][j] est l’énergie minimum d’un chemin depuis le haut de l’image jusqu’à un pixel i, j.

Solution

def dp_chemin(g):
    d = np.zeros(g.shape)
    d[0] = g[0]
    for i in range(1, g.shape[0]):
        d[i, 0] = g[i, 0] + min(d[i-1, 0], d[i-1, 1])
        d[i, -1] = g[i, -1] + min(d[i-1, -1], d[i-1, -2])
        for j in range(1, g.shape[1]-1):
            d[i, j] = g[i, j] + min(d[i-1, j-1], d[i-1, j], d[i-1, j+1])
    return d

d = dp_chemin(matrice_gradient(m))
plt.imshow(d, cmap='gray') # affichage de d : plus un pixel est sombre, plus il est facile de le supprimer
plt.show()

On veut maintenant trouver un chemin vertical d’énergie minimum à partir de la matrice d de la question précédente.
Pour cela, on construit le chemin à l’envers : on commence par chercher le pixel de la dernière ligne (tout en bas) d’énergie minimale, puis on remonte.

Question

Écrire une fonction min_energie_bas(d) qui renvoie le numéro de colonne j du pixel de la dernière ligne d’énergie minimale, c’est-à-dire tel que d[n - 1][j] est minimal, où d est la matrice renvoyée par la fonction dp_chemin(m) et n est le nombre de lignes de d.

Solution

def min_energie_bas(d):
    j_mini = 0 # indice du minimum de d sur la dernière ligne
    for j in range(1, d.shape[1]):
        if d[-1, j] < d[-1, j_mini]:
            j_mini = j
    return j_mini

min_energie_bas(d)

705

Question

Écrire une fonction min_chemin(m) qui renvoie un chemin c vertical d’énergie minimum dans une image m. Ainsi, c[i] est le numéro de colonne du pixel de la ligne i du chemin. d est la matrice renvoyée par la fonction dp_chemin(m).

def min_chemin(m):
    d = dp_chemin(matrice_gradient(m))
    c = [min_energie_bas(d)]
    for i in range(len(m) - 2, -1, -1): # parcours de la dernière ligne à la première
        j = c[-1] # position du chemin sur la ligne i+1
        mini = ... 
        ... # trouver le minimum de d[i, j-1], d[i, j], d[i, j+1]
        c.append(mini)
    return c[::-1] # pour inverser c

Solution

def min_chemin(m):
    d = dp_chemin(matrice_gradient(m))
    c = [min_energie_bas(d)]
    for i in range(len(m) - 2, -1, -1):
        j = c[-1]
        mini = j
        for k in range(j - 1, j + 2):
            if k >= 0 and k < len(d[i]) and d[i, k] < d[i, j]:
                mini = k
        c.append(mini)
    return c[::-1] # pour inverser c

c = min_chemin(m)
plt.imshow(m, cmap='gray')
plt.plot(c, range(len(c)), 'r', linewidth=1); # affichage de l'image avec le chemin en rouge
plt.show()
c[:10] # affichage des 10 premières valeurs de c

[702, 702, 702, 701, 701, 700, 699, 698, 697, 696]

Question

Écrire finalement une fonction seam_carving(m, n) qui réalise \(n\) fois les instructions suivantes :

• Calculer la matrice g des gradients de m

• Calculer un chemin c d’énergie minimum dans g

• Enlever le chemin c de m

Solution

def seam_carving(m, n):
    for i in range(n):
        c = min_chemin(m)
        m = enlever_chemin(m, c)
    return m

seam_carving_im = seam_carving(m, 200) # on enlève 200 colonnes (cela prend un peu de temps)
plt.imshow(seam_carving_im, cmap='gray')
plt.show()
np.shape(seam_carving_im) # l'image a bien été redimensionnée

(484, 514)

Bonus

Question

Modifier les fonctions précédentes pour redimensionner suivant la hauteur et non la largeur.

Question

Tester avec l’image de votre choix.