Algorithme des k-moyennes

[Visualisation de l'algorithme des k-moyennes](https://www.naftaliharris.com/blog/visualizing-k-means-clustering)

Génération des données

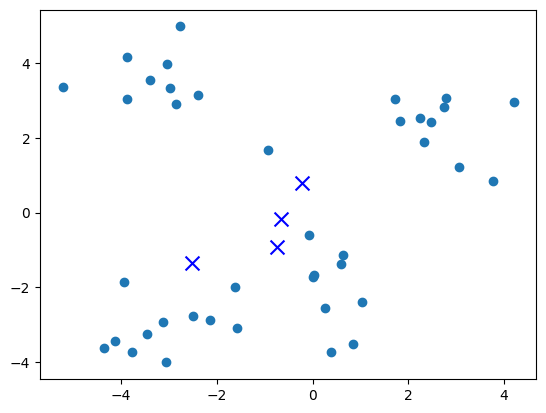
On génère des points aléatoirement, ainsi que k = 4 centres initialement aléatoires :

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap

k, dim = 4, 2
X = np.vstack([np.array(p + np.random.randn(10, dim)) for p in [[3, 2], [0, -2], [-3, 3], [-3, -3]]]).tolist()
centres = (np.random.rand(k, dim)*6 - 3).tolist()
plt.scatter([x[0] for x in X], [x[1] for x in X])
plt.scatter([x[0] for x in centres], [x[1] for x in centres], marker='x', s=100, c='b')
plt.show()

Code

def centre(X):
    c = [0.]*dim
    for x in X:
        for i in range(len(x)):
            c[i] += x[i]
    if len(X) == 0: return c
    for i in range(len(c)):
        c[i] /= len(X)
    return c

def calculer_centres(classes):
    centres = []
    for i in range(len(classes)):
        centres.append(centre(classes[i]))
    return centres

def d(x, y):
    s = 0.
    for i in range(len(x)):
        s += (x[i] - y[i])**2
    return s**.5

def plus_proche(x, centres):
    imin = 0
    for i in range(len(centres)):
        if d(x, centres[i]) < d(x, centres[imin]):
            imin = i
    return imin

def calculer_classes(X, centres):
    classes = [[] for i in range(len(centres))]
    for x in X:
        classes[plus_proche(x, centres)].append(x)
    return classes

def kmeans(X, centres):
    centres2 = None
    while centres != centres2:
        centres2 = centres
        classes = calculer_classes(X, centres2)
        centres = calculer_centres(classes)
    return classes

def inertia(classes, centres):
    s = 0.
    for i in range(len(centres)):
        for x in classes[i]:
            s += d(x, centres[i])**2
    return s

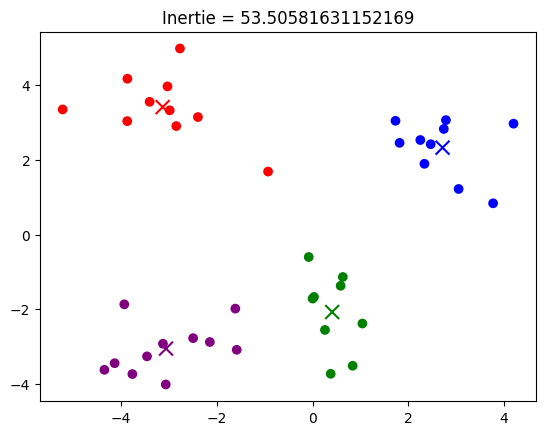
Test

classes = kmeans(X, centres) # test de kmeans

cmap = ListedColormap(['r', 'g', 'b', 'purple'])
centres = calculer_centres(classes)
plt.scatter([x[0] for x in X], [x[1] for x in X], c=[plus_proche(x, centres) for x in X], cmap=cmap)
plt.scatter([x[0] for x in centres], [x[1] for x in centres], marker='x', s=100, c=range(k), cmap=cmap)
plt.title("Inertie = " + str(inertia(classes, centres)))
plt.show()

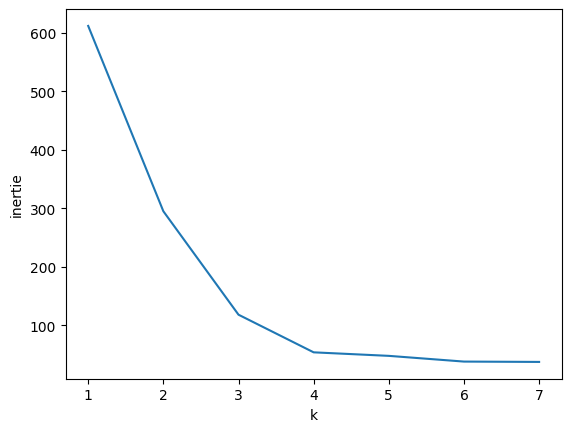
elbow method

kmax = 7
inertie = []
for k in range(1, kmax+1):
    centres = (np.random.rand(k, dim)*6 - 3).tolist()
    classes = kmeans(X, centres)
    centres = calculer_centres(classes)
    inertie.append(inertia(classes, centres))
plt.plot(range(1, kmax+1), inertie)
plt.xlabel("k")
plt.ylabel("inertie")
plt.show()

Animation

from pathlib import Path
from scipy.spatial import Voronoi, voronoi_plot_2d

p = 3
X = np.vstack([np.array(p + np.random.randn(10, 2)) for p in [[3, 2], [0, -2], [-3, 3]]])
centres, new_centres, classes = np.random.rand(3, 2)*6 - 3, None, None

def scatter(X, **kwargs): plt.scatter(X[:,0], X[:,1], cmap=ListedColormap(['r', 'g', 'b']), **kwargs)
def save(title):
    global p
    scatter(centres, marker='x', s=100, c=[0, 1, 2])
    scatter(X, c=classes)
    plt.title(title)
    plt.savefig(f'img/kmean_{p}.png')
    p += 1
def d(a, b): return np.sum((a-b)**2)

for f in Path('img').glob('*.png'): f.unlink()
scatter(X)
plt.title("Données que l'on souhaite classifier")
plt.savefig(f'img/kmean_1.png')
scatter(centres, marker='x', s=100, c=[0, 1, 2])
plt.title("Choix initial des centres")
plt.savefig(f'img/kmean_2.png')

while True:
    classes = np.array([np.argmin([d(x, c) for c in centres]) for x in X])
    plt.clf()
    save("Association de chaque donnée au centre le plus proche")

    new_centres = np.array([X[classes==i].mean(axis=0) for i in range(3)])
    if np.allclose(centres, new_centres): break

    centres = new_centres
    plt.clf()
    save("Mise à jour des centres")

ax = plt.gca()
x, y = ax.get_xlim(), ax.get_ylim()
vor = Voronoi(centres)
voronoi_plot_2d(vor, ax, show_points=False, show_vertices=False)
ax.set_xlim(x)
ax.set_ylim(y)
save("Frontière de décision")

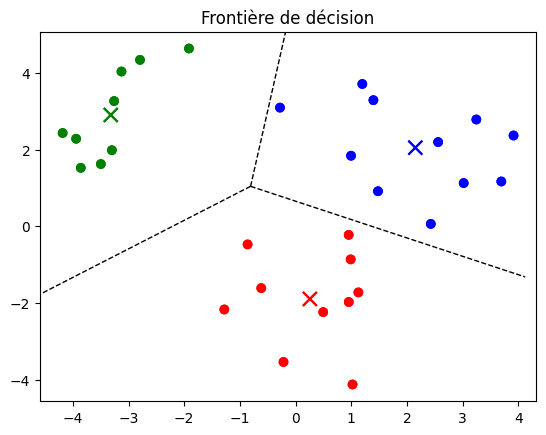
Compression d’image

from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
import numpy as np

img = plt.imread('compression/parrot.jpg')
plt.imshow(img)
plt.show()

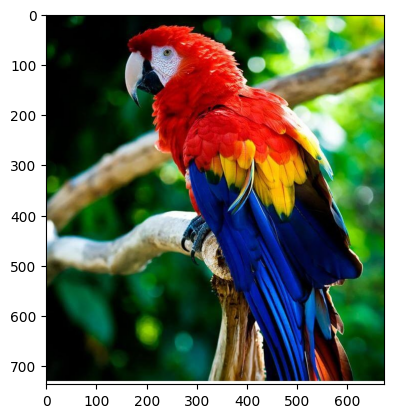
pixels = img.reshape(-1, 3)
print(f"pixels contient {len(pixels)} pixels de 3 couleurs chacun")
kmeans = KMeans(n_clusters=8, random_state=0).fit(pixels)
print(f"Centres des 8 clusters de pixels : {kmeans.cluster_centers_}")
print(f"kmeans.labels_ contient les classes de chaque pixel : {kmeans.labels_}")
img_compressed = kmeans.cluster_centers_[kmeans.labels_].astype('uint8')
print(f"img_compressed est obtenu à partir de pixels en remplaçant chaque pixel par le centre de son cluster")
img_compressed = img_compressed.reshape(img.shape)
plt.axis('off')
plt.imshow(img_compressed)
plt.show()
plt.imsave('compression/parrot_compressed.png', img_compressed)

pixels contient 496738 pixels de 3 couleurs chacun
Centres des 8 clusters de pixels : [[  7.66165195  19.76974168  10.35961169]
 [164.1427278  177.25148203 142.0176766 ]
 [107.72793283 127.07565615  47.67371984]
 [207.45478823 170.16388681  32.67841079]
 [  9.0873963   41.5624455  135.5594808 ]
 [195.67637004  24.02326738  14.00799751]
 [223.28612846 234.53746655 225.07193832]
 [ 13.17134015  99.70298247  39.31646374]]
kmeans.labels_ contient les classes de chaque pixel : [0 0 0 ... 6 6 6]
img_compressed est obtenu à partir de pixels en remplaçant chaque pixel par le centre de son cluster

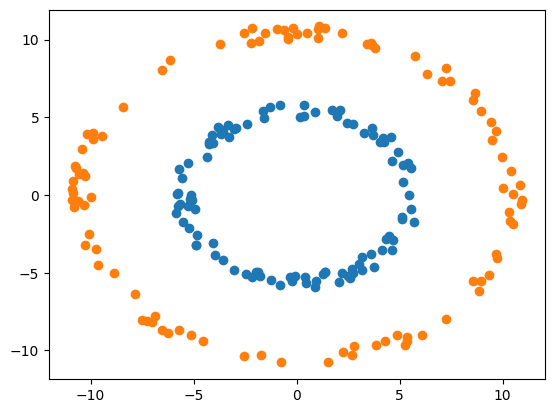
Exemple de problème non linéairement séparable

import numpy as np
import matplotlib.pyplot as plt

theta = np.random.rand(100)*2*np.pi
r1 = 10 
r2 = 5 + np.random.rand(100)
for k in [5, 10]:
    r = k + np.random.rand(100)
    theta = np.random.rand(100)*2*np.pi
    plt.scatter(r*np.cos(theta), r*np.sin(theta))