TP : Reconnaissance de chiffres
Contents
TP : Reconnaissance de chiffres#

Remarque : le jeu de données utilisé est normalement utilisé pour de la classification supervisée (puisque les classes sont déjà connues) mais il est quand même intéressant d’utiliser l’algorithme des k-moyennes (qui est non-supervisé) pour voir s’il arrive à trouver les classes correspondants aux chiffres.
Commençons par charger les données :
import numpy as np
from sklearn.datasets import load_digits
from matplotlib import pyplot as plt
digits = load_digits()
digits_matrix = digits.images[1000:] # utilisation d'une partie seulement pour accélérer les calculs
digits_matrix.shape
(797, 8, 8)
digits_matrix est un tableau numpy de taille \(797\times 8\times 8\), c’est-à-dire \(797\) matrices de taille \(8\times 8\).
digits_matrix[0] # la 1ère matrice
array([[ 0., 0., 1., 14., 2., 0., 0., 0.],
[ 0., 0., 0., 16., 5., 0., 0., 0.],
[ 0., 0., 0., 14., 10., 0., 0., 0.],
[ 0., 0., 0., 11., 16., 1., 0., 0.],
[ 0., 0., 0., 3., 14., 6., 0., 0.],
[ 0., 0., 0., 0., 8., 12., 0., 0.],
[ 0., 0., 10., 14., 13., 16., 8., 3.],
[ 0., 0., 2., 11., 12., 15., 16., 15.]])
Chacune de ces matrices est en fait une image de \(8\times 8\) pixels, représentant un chiffre manuscrit.
Chaque élément de la matrice représente un niveau de gris entre \(0\) (blanc) et \(16\) (noir).
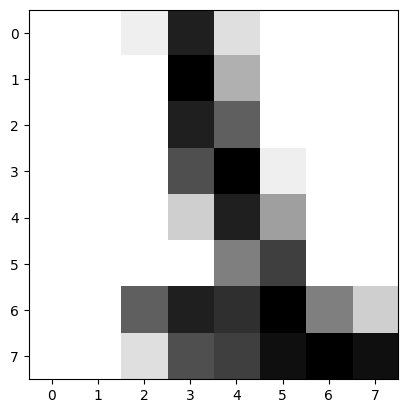
Par exemple, affichons l’image correspondant à la matrice ci-dessus :
plt.imshow(digits_matrix[0], cmap=plt.cm.gray_r)
plt.show() # ça ressemble à un 1
Redimensionner les images#
Pour appliquer l’algorithme des \(k\)-moyennes, il faut que les données soient des vecteurs. On transforme donc une matrice en vecteur en concaténant les lignes de la matrice :
$\(
\begin{pmatrix}
1 & 2 & 3 \\
4 & 5 & 6 \\
7 & 8 & 9
\end{pmatrix}
\longrightarrow
\begin{pmatrix}
1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9
\end{pmatrix}
\)$
Question
Écrire une fonction to_vector(m) qui prend en argument une matrice m et renvoie le vecteur correspondant, sous forme de liste.
Solution
def to_vector(m):
v = []
for i in range(0,8):
for j in range(0,8):
v.append(m[i][j])
return v
assert len(to_vector(digits_matrix[0])) == 64 # les images 8*8 sont transformées en vecteur 64
Question
Écrire une fonction to_matrix(v) qui prend en argument un vecteur v et renvoie la matrice correspondante, sous forme de liste de listes. On suppose que la matrice est carrée.
Solution
def to_matrix(vector):
mat = [[0 for i in range(0, 8)] for j in range(0, 8)]
for i in range(0, 8):
for j in range(0, 8):
mat[i][j] = vector[i*8+j]
return mat
assert (to_matrix(to_vector(digits_matrix[0])) == digits_matrix[0]).all()
# to_matrix et to_vector sont inverses l'une de l'autre
Question
Définir une liste X contenant les vecteurs correspondant aux images dans digits_matrix. Cette variable X sera utilisée dans toute la suite.
Solution
X = []
for i in range(0, len(digits_matrix)):
X.append(to_vector(digits_matrix[i]))
Algorithmes des \(k\)-moyennes#
Question
Écrire une fonction d(u, v) qui prend en argument deux vecteurs u et v et renvoie la distance euclidienne entre ces deux vecteurs.
Solution
def d(u, v):
s = 0
for i in range(0, len(u)):
s += (u[i] - v[i])**2
return s**.5
d([1, 2, 3], [4, 5, 6])
5.196152422706632
Comme dans le cours, nous utilisons une liste centres pour stocker les centres des classes. centres[i] est le centre de la classe \(i\).
Question
Écrire une fonction centres_aléatoires(X, k) qui prend en argument une liste de vecteurs X et un entier k et renvoie une liste de k vecteurs aléatoires choisis dans X.
On utilisera random.sample dont on pourra consulter la documentation ici. On pourra préalablement utiliser random.seed(0) pour avoir les mêmes résultats que le corrigé du TP.
Solution
import random
random.seed(0) # pour avoir toujours les mêmes résultats
def centres_aléatoires(X, k):
return random.sample(X, k)
centres = centres_aléatoires(X, 10)
assert len(centres) == 10 and len(centres[0]) == 64
Question
Écrire une fonction plus_proche(x, centres) qui prend en argument un vecteur x et une liste de vecteurs centres et renvoie l’indice du centre le plus proche de x.
Solution
def plus_proche(x, centres):
return min(range(len(centres)), key=lambda i: d(x, centres[i]))
plus_proche([1, 2], [[4, 5], [2, 3], [4, 0]])
1
Contrairement à ce qui a été fait dans le cours, on utilise dans la suite une liste classes telle que classes[i] est le numéro de classe de X[i] (dans le cours, classes[i] était la liste des vecteurs de la classe \(i\)).
Question
Écrire une fonction calculer_classes(X, centres) qui renvoie la liste classes correspondant à X et à centres. Il faut donc que classes[i] soit l’indice du centre (dans centres) le plus proche de X[i].
Solution
def calculer_classes(X, centres):
classes = []
for x in X:
classes.append(plus_proche(x, centres))
return classes
classes = calculer_classes(X, centres_aléatoires(X, 10))
assert len(classes) == len(X) and max(classes) < 10 and min(classes) >= 0
Question
Écrire une fonction centre(X, classes, i) qui renvoie le centre de la classe \(i\).
Solution
def centre(X, classes, i):
p = len(X[0])
c = [0]*p
n = 0
for j in range(len(X)):
if classes[j] == i:
n += 1
for k in range(p):
c[k] += X[j][k]
for k in range(p):
c[k] /= n
return c
assert len(centre(X, classes, 0)) == 64
Question
Écrire une fonction calculer_centres(X, classes, k) qui renvoie la liste centres correspondant à X et à classes.
Solution
def calculer_centres(X, classes, k):
centres = []
for i in range(0, k):
centres.append(centre(X, classes, i))
return centres
classes = calculer_classes(X, centres_aléatoires(X, 10))
assert len(calculer_centres(X, classes, 10)) == 10 and len(calculer_centres(X, classes, 10)[0]) == 64
Question
Écrire une fonction kmeans(X, centres, k) qui, à partir de centres initiaux donnés en argument, applique l’algorithme des \(k\)-moyennes et renvoie un couple correspondant à la liste (centres, classes) obtenue à la fin de l’algorithme.
Solution
def kmeans(X, centres, k):
classes = calculer_classes(X, centres)
centres = calculer_centres(X, classes, k)
if classes != calculer_classes(X, centres):
return kmeans(X, centres, k)
return centres, classes
k = 10
centres, classes = kmeans(X, centres_aléatoires(X, k), k) # ceci prend quelques secondes
fig, axes = plt.subplots(2, 5, figsize=(8, 3))
for ax, center in zip(axes.ravel(), centres):
ax.matshow(np.array(to_matrix(center)).reshape((8, 8)), cmap=plt.cm.gray_r)
ax.axis('off')
plt.show()
Calcul de l’inertie#
Dans cette partie, on réutilise les listes centres et classes obtenues précédemment par un appel à kmeans.
Question
Écrire une fonction inertie(X, centres, classes) qui renvoie l’inertie de la partition définie par classes. On rappelle que l’inertie d’une partition est la somme des distances au carré des points à leur centre de classe.
Solution
def inertie(X, centres, classes):
s = 0
for i in range(len(X)):
s += d(X[i], centres[classes[i]])**2
return s
inertie(X, centres, classes)
497072.30362746114
Question
Réécrire la fonction kmeans précédente de façon à ce qu’elle renvoie aussi la liste des inerties obtenues à chaque itération de l’algorithme. Utiliser le code ci-dessous pour afficher aussi l’évolution de l’inertie au cours des itérations. Commenter.
Solution
def kmeans(X, centres, k):
inerties = []
centres2 = None
while centres != centres2:
centres2 = centres
classes = calculer_classes(X, centres2)
centres = calculer_centres(X, classes, k)
inerties.append(inertie(X, centres, classes))
return centres, classes, inerties
centres, classes, inerties = kmeans(X, centres_aléatoires(X, k), k) # ceci prend quelques secondes
plt.plot(inerties)
plt.show()
Classification de nouvelles images#
Question
Exécuter le code suivant pour afficher le centre de chaque classe. Il s’agit donc, pour chaque classe, de l’image obtenue en faisant la moyenne (pixel par pixel) des images de la classe.
fig, axes = plt.subplots(2, 5, figsize=(8, 3))
for ax, center in zip(axes.ravel(), centres):
ax.matshow(np.array(to_matrix(center)).reshape((8, 8)), cmap=plt.cm.gray_r)
ax.axis('off')
plt.show()
Sur l’image ci-dessus, les classes sont représentés dans l’ordre, de gauche à droite et de haut en bas. Par exemple, l’image en haut à gauche correspond à la classe \(0\), celle juste à droite à la classe \(1\)…
Question
Définir une liste classe_to_chiffre telle que classe_to_chiffre[i] est le chiffre que vous pouvez lire pour le centre de la classe \(i\).
Solution
classe_to_chiffre = [1, 9, 5, 7, 5, 6, 4, 2, 4, 0]
Question
Exécuter le code suivant pour stocker dans X_test les vecteurs correspondant aux images que l’on va essayer de classifier, en utilisant le résultat de kmeans.
X_test = list(map(to_vector, digits.images[:500]))
Exercice
Écrire une fonction
predict(x, centres, classe_to_chiffre)qui renvoie le chiffre prédit pour l’imagex. Il faut donc trouver la classeila plus proche dexet renvoyerclasse_to_chiffre[i].Exécuter le code suivant pour afficher des images de
X_testet les chiffres prédits.
Solution
def predict(x, centres, classe_to_chiffre):
return classe_to_chiffre[plus_proche(x, centres)]
fig, axes = plt.subplots(2, 5, figsize=(8, 5))
for i, ax in enumerate(axes.ravel()):
ax.matshow(np.array(to_matrix(X[i])).reshape((8, 8)), cmap=plt.cm.gray_r)
ax.set_title(predict(X[i], centres, classe_to_chiffre))
ax.axis('off')
plt.show()
Question
Écrire une fonction precision(centres) qui renvoie la précision de cet algorithme de classification, sur les données de X_test. Pour cela, on compte la proportion de classe prédite pour X_test[i] égale à digits.target[i].
Solution
def precision(centres):
n = 0
for i in range(len(X_test)):
if predict(X_test[i], centres, classe_to_chiffre) == digits.target[i]:
n += 1
return n/len(X_test)
precision(centres)
0.664
Avec les \(k\) plus proches voisins#
Question
Implémenter l’algorithme des \(k\) plus proches voisins et comparer la précision obtenue avec celle des \(k\)-moyennes. Quel algorithme de classification semble le plus adapté ici ?


