TP : Dictionnaire

Internationalisation

Exercice

1. Définir un dictionnaire fr_to_en contenant chaque jour de la semaine (en français) avec sa traduction en anglais.

2. Vérifier que fr_to_en["lundi"] contient "monday".

3. Ajouter les mois avec leurs traductions.

Solution

# 1.
fr_to_en = {"lundi": "Monday", "mardi": "Tuesday", "mercredi": "Wednesday", "jeudi": "Thursday", "vendredi": "Friday", "samedi": "Saturday", "dimanche": "Sunday"}

# 2.
print(fr_to_en["lundi"])

# 3. On peut utiliser une boucle for pour simplifier
for m1, m2 in [("janvier", "January"), ("février", "February"), ("mars", "March"), ("avril", "April"), ("mai", "May"), ("juin", "June"), ("juillet", "July"), ("août", "August"), ("septembre", "September"), ("octobre", "October"), ("novembre", "November"), ("décembre", "December")]:
    fr_to_en[m1] = m2

fr_to_en["janvier"]

'January'

Élément majoritaire

Exercice

Écrire une fonction majoritaire(L) renvoyant l’élément apparaissant le plus souvent dans la liste L, sans utiliser de dictionnaire. Quelle est sa complexité ?

Solution

# en utilisant count :
def majoritaire(L):
    m = L[0] # va contenir l'élément majoritaire
    for e in L:
        if L.count(e) > L.count(m):
            m = e
    return m

# sans utiliser count :
def majoritaire(L):
    m, n = None, 0 # va contenir l'élément majoritaire et son nombre d'occurences
    for e in L:
        n = 0
        for f in L:
            if f == e:
                n += 1
        if n > L.count(m):
            m = e
    return m

# dans les deux cas, la complexité est O(n^2), où n est la longueur de la liste L

majoritaire([9, 1, 9, 0, 1, 1, 0])

1

Exercice

Écrire une fonction majoritaire2(L) renvoyant l’élément apparaissant le plus souvent dans la liste L, en utilisant un dictionnaire pour avoir une meilleure complexité que la fonction précédente.

Solution

# Fonction écrite en cours. La complexité est O(n), où n est la longueur de la liste L.

def majoritaire2(L):
    d = {}
    for e in L:
        if e in d:
            d[e] += 1
        else:
            d[e] = 1
    m = L[0]
    for e in d:
        if d[e] > d[m]:
            m = e
    return m

majoritaire2([9, 1, 9, 0, 1, 1, 0])

1

Anagramme

On rappelle qu’on peut parcourir les lettres d’une chaîne de caractères avec une boucle for :

s = "lamartin"
for c in s: # en parcourant directement les caractères
    print(c)
for i in range(len(s)): # en parcourant les indices
    print(s[i])

Exercice

Écrire une fonction anagramme(m1, m2) qui teste si deux mots (des chaînes de caractères) sont des anagrammes, c’est-à-dire s’ils contiennent les mêmes lettres (avec le même nombre d’occurence de chaque lettre).
Cette fonction doit être en O(\(n_1 + n_2\)), où \(n_1\), \(n_2\) sont les tailles de m1, m2.

Solution

def anagramme(m1, m2):
    d1, d2 = {}, {}
    for c in m1: # O(n1)
        if c in d1:
            d1[c] += 1
        else:
            d1[c] = 1
    for c in m2: # O(n1)
        if c in d2:
            d2[c] += 1
        else:
            d2[c] = 1
    return d1 == d2 # O(n1)

print(anagramme("ordre", "dorer"))
print(anagramme("ordre", "oreo"))

True
False

Trie (arbre préfixe)

Arbres enracinés

Un arbre est un graphe ayant deux propriétés supplémentaires :

• Connexe : il existe un chemin entre deux sommets quelconques

• Acyclique : il ne contient pas de cycle

On considère souvent des arbres enracinés, c’est-à-dire ayant un sommet particulier appelé la racine, qu’on représente en haut de l’arbre :

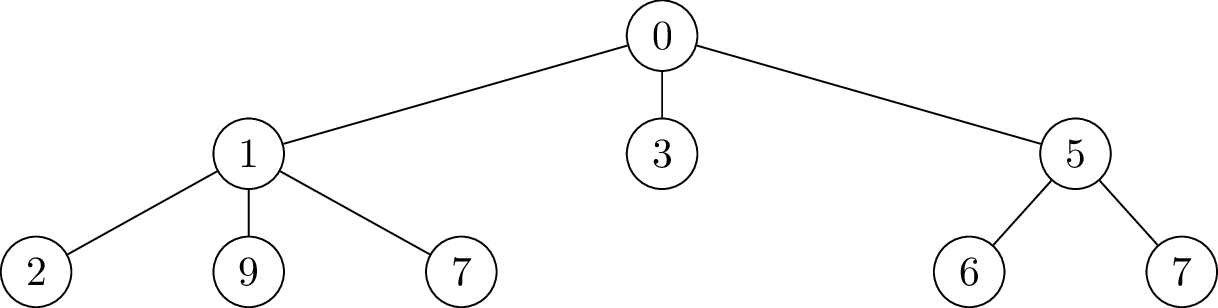
Exemple d'arbre, ayant pour racine 0

Chaque sommet différent de la racine possède un père, qui est le sommet juste au dessus. Sur l’exemple, 0 est le père de 1, 1 est le père de 7…

Si p est le père de v, on dit aussi que v est un fils de p. Chaque sommet a au plus un père, mais peut avoir un nombre quelconque de fils.

Trie

Un trie sert à stocker un ensemble de mots sous forme d’arbre. Chaque arête est etiquetée par une lettre et les mots appartenant au trie sont ceux obtenus le long d’un chemin de la racine à une arête étiquetée par $.
Par exemple, l’arbre suivant contient les mots cap, copie, copier, copies, cor, corde, corne, correct, correcte :

Remarque : les tries sont utilisés pour la complétion automatique (proposition de complétion d’un mot en cours d’écriture, par exemple sur téléphone), pour la correction orthographique…

Pour stocker un trie, on utilisera un dictionnaire où chaque clé est l’étiquette d’une arête sortant de la racine et la valeur est le dictionnaire correspondant au fils. Une feuille (sommet sans fils) est représentée par le dictionnaire vide.

Par exemple, le trie contenant l’ensemble de mots \(\{\) car, cat, cd, ok \(\}\) est représenté par :

trie_ex = { 
    "c" : { 
        "a" : {
            "r" : { "$" : {} },
            "t" : { "$" : {} }
        },
        "d" : { "$" : {} }
    },
    "o" : { 
        "k" : { "$" : {} }
    }
}
trie_ex

{'c': {'a': {'r': {'$': {}}, 't': {'$': {}}}, 'd': {'$': {}}},
 'o': {'k': {'$': {}}}}

Exercice

1. Dessiner le trie contenant les mots art, axe, set.

2. Définir ce trie sous forme d’un dictionnaire.

Solution

trie = {
    "a": {
        "r": {
            "t": { "$" : {} },
        },
        "x": {
            "e": { "$" : {} },
        },
    },
    "s": {
        "e": {
            "t": { "$" : {} },
        },
    },
}

Exercice

Écrire une fonction trie_size(trie) pour afficher le nombre de mots appartenant à un trie. Pour cela, on parcourt récursivement le trie en comptant le nombre de $.

def trie_size(trie):
    n = 0 # compte le nombre de $
    for k in trie:
        ...
    return n

Solution

def trie_size(trie):
    n = 0
    for k in trie:
        if k == '$':
            n += 1
        else:
            n += trie_size(trie[k])
    return n

trie_size(trie_ex)

4

Exercice

Écrire une fonction trie_add(trie, m) pour ajouter un mot m dans un trie. On pourra compléter le code ci-dessous.

def trie_add(trie, m):
    for c in m: # parcours des lettres c de m
        if ...: # s'il n'y a pas d'arête sortante de trie étiquetée par c
            ... # créer une nouvelle association (c, dictionnaire vide)
        trie = trie[c] # descendre dans l'arbre suivant la lettre c
    ... # ajouter un '$' à la fin

Solution

def trie_add(trie, m):
    for c in m:
        if c not in trie:
            trie[c] = dict()
        trie = trie[c]
    trie['$'] = dict()

trie = {}
trie_add(trie, "arbre")
trie_add(trie, "arete")
trie

{'a': {'r': {'b': {'r': {'e': {'$': {}}}}, 'e': {'t': {'e': {'$': {}}}}}}}

Exercice

Écrire une fonction trie_print(trie) pour afficher les mots m appartenant à un trie. Vérifier avec l’exemple précédent.
On pourra utiliser une fonction auxiliaire récursive aux(t, m) qui s’appelle récursivement sur chaque noeud t du trie, en conservant les lettres déjà parcourues dans la chaîne de caractères m.

def trie_print(trie):
    def aux(t, m):
        ...
    aux(trie, "")

Solution

def trie_print(trie):
    def aux(t, m):
        for k in t:
            if k == '$':
                print(m)
            else:
                aux(t[k], m + k)
    aux(trie, "")

trie_print(trie_ex)

car
cat
cd
ok

Exercice

Écrire une fonction trie_has(trie, m) pour tester si m appartient à un trie.

Solution

def trie_has(trie, mot):
    def aux(t, m, i): # t est le sous-arbre, m est le mot recherché, i est l'indice de la lettre courante
        if i == len(m):
            return '$' in t
        if m[i] not in t:
            return False
        return aux(t[m[i]], m, i + 1)
    return aux(trie, mot, 0)

print(trie_has(trie_ex, "carte"))
print(trie_has(trie_ex, "car"))

False
True