Algorithme min-max
Contents
Algorithme min-max#
Implémentation#
def minmax(s, h, v, p, joueur):
succ = [minmax(s, h, w, p - 1, 1 - joueur) for w in s(v, joueur)]
if succ == [] or p == 0:
return h(v)
if joueur == 0:
return max(succ)
else:
return min(succ)
Application au jeu du domineering#
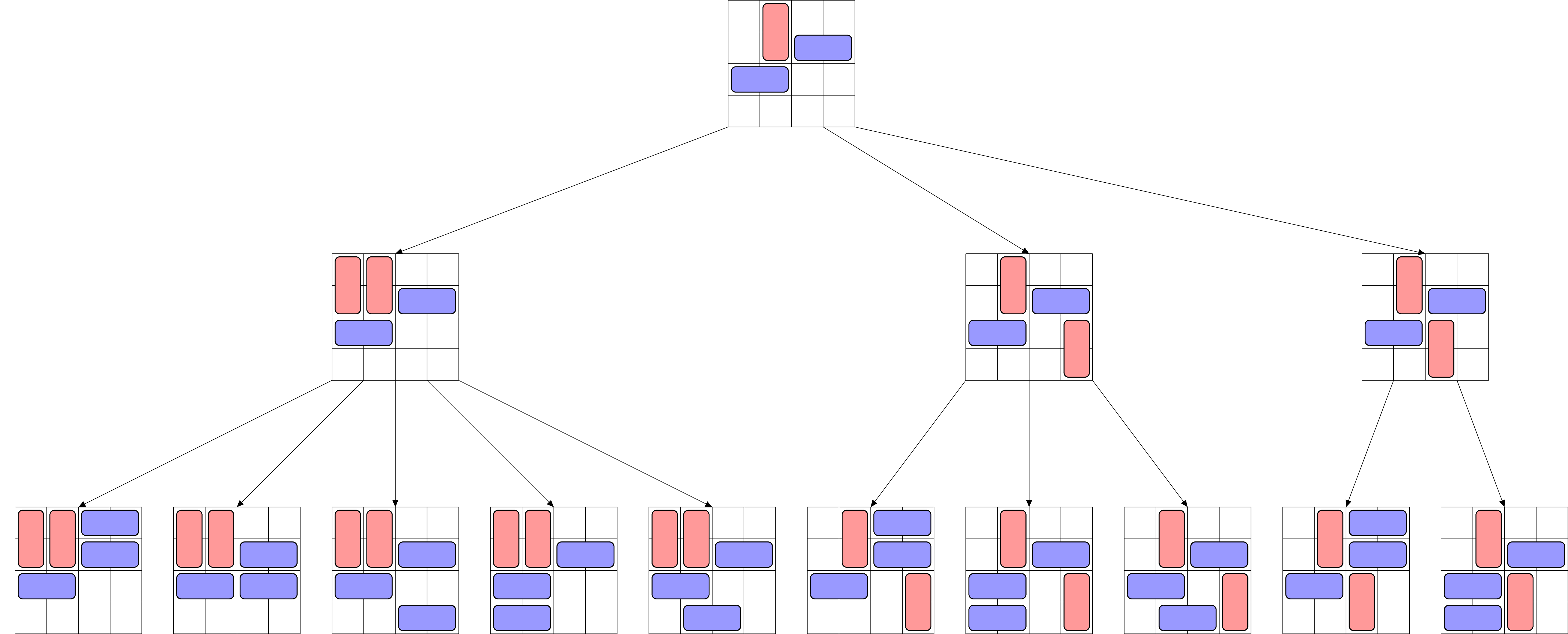
import numpy as np
v = -np.ones((4, 4))
v[0][1] = v[1][1] = 0
v[1][2] = v[1][3] = v[2][0] = v[2][1] = 1
v # représentation du plateau initial
array([[-1., 0., -1., -1.],
[-1., 0., 1., 1.],
[ 1., 1., -1., -1.],
[-1., -1., -1., -1.]])
Heuristique#
def h(v):
n0, n1 = 0, 0 # nombre de possibilités pour les deux joueurs
for i in range(len(v)):
for j in range(len(v[0])):
if i + 1 < len(v) and v[i][j] == v[i + 1][j] == -1:
n0 += 1
if j + 1 < len(v[0]) and v[i][j] == v[i][j + 1] == -1:
n1 += 1
if n0 == 0:
return -float('inf')
if n1 == 0:
return float('inf')
return n0 - n1
h(v) # test
-2
Successeurs#
import copy
def s(v, joueur):
succ = []
for i in range(4):
for j in range(4):
if v[i][j] == -1:
w = copy.deepcopy(v)
if joueur == 0 and i < 3 and v[i + 1][j] == -1:
w[i][j] = w[i + 1][j] = joueur
succ.append(w)
if joueur == 1 and j < 3 and v[i][j + 1] == -1:
w[i][j] = w[i][j + 1] = joueur
succ.append(w)
return succ
s(v, 0)
[array([[ 0., 0., -1., -1.],
[ 0., 0., 1., 1.],
[ 1., 1., -1., -1.],
[-1., -1., -1., -1.]]),
array([[-1., 0., -1., -1.],
[-1., 0., 1., 1.],
[ 1., 1., 0., -1.],
[-1., -1., 0., -1.]]),
array([[-1., 0., -1., -1.],
[-1., 0., 1., 1.],
[ 1., 1., -1., 0.],
[-1., -1., -1., 0.]])]
Test#
minmax(s, h, v, 2, 0) # test
1
On retrouve donc bien le bon résultat :
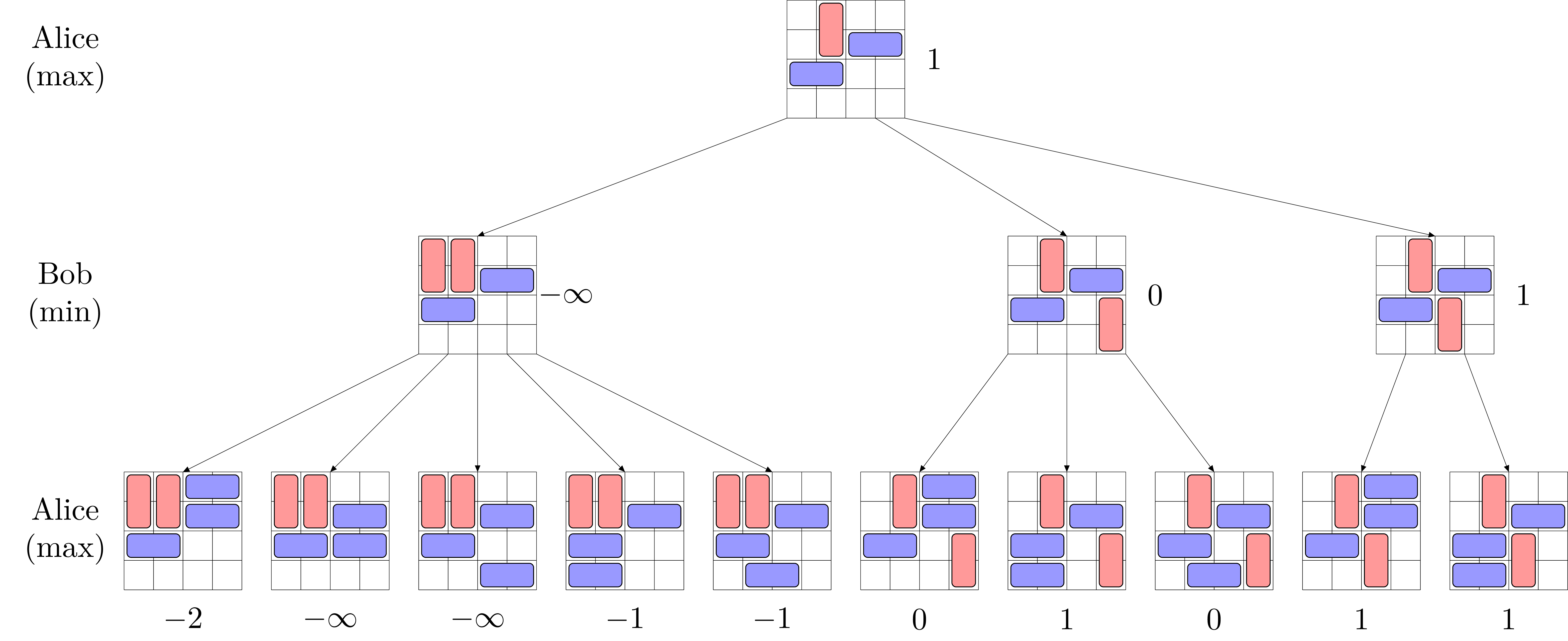
Calcul du coup suivant#
def minmax(s, h, v, p, joueur): # renvoie (coup à jouer, valeur de la position v)
succ = s(v, joueur)
if succ == [] or p == 0:
return v, h(v)
if joueur == 0:
hmax = None
for u in succ:
_, hu = minmax(s, h, u, p - 1, 1 - joueur)
if hmax is None or hu > hmax:
umax, hmax = u, hu
return umax, hmax
else:
hmin = None
for u in succ:
_, hu = minmax(s, h, u, p - 1, 1 - joueur)
if hmin is None or hu < hmin:
umin, hmin = u, hu
return umin, hmin
Affichage des coups choisis par min-max#
import matplotlib.pyplot as plt
from matplotlib.patches import Rectangle
def affiche(v):
n = len(v)
ax = plt.axes(xlim=(0, n), ylim=(0, n))
ax.set_aspect('equal', 'box')
plt.xticks(range(5))
plt.yticks(range(5))
plt.grid()
for i in range(n):
for j in range(n):
if v[i][j] == 0:
ax.add_patch(Rectangle((j, n - 1 - i), 1, 1, facecolor='red'))
if v[i][j] == 1:
ax.add_patch(Rectangle((j, n - 1 - i), 1, 1, facecolor='blue'))
plt.show()
v
array([[-1., 0., -1., -1.],
[-1., 0., 1., 1.],
[ 1., 1., -1., -1.],
[-1., -1., -1., -1.]])
def jeu(s, h, v, p, joueur):
affiche(v)
if s(v, joueur) == []:
print(f"Joueur {1 - joueur} a gagné")
return
u, hu = minmax(s, h, v, p, joueur)
jeu(s, h, u, p, 1 - joueur)
# g = -np.ones((4, 4))
jeu(s, h, v, 3, 0)
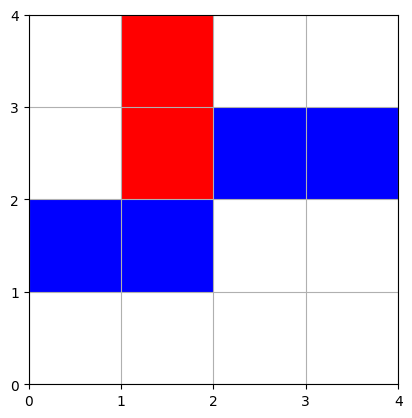
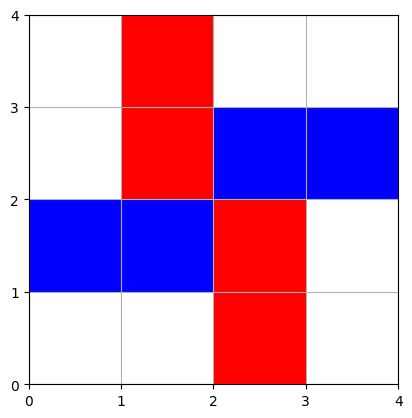
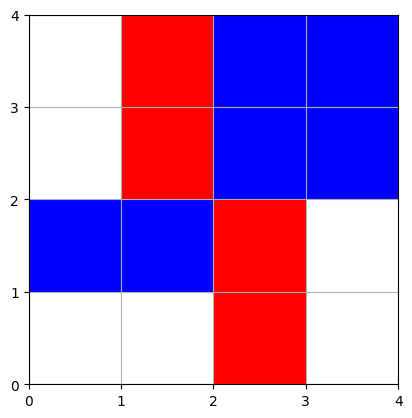
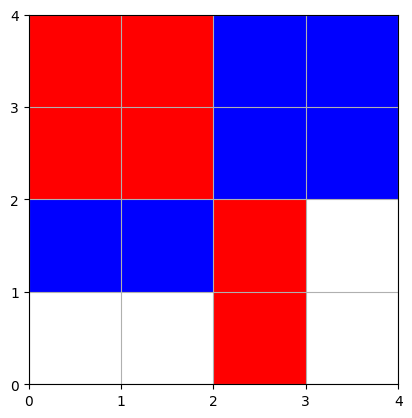
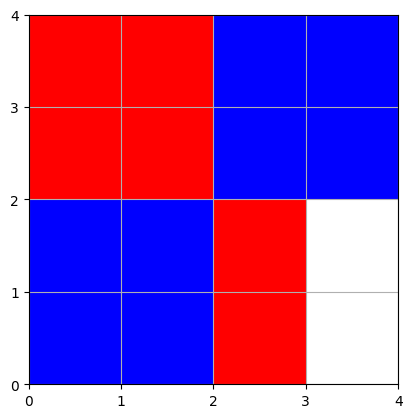
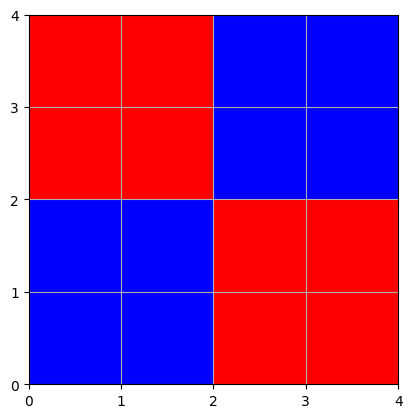
Joueur 0 a gagné


