TP : Classification de voitures
Contents
TP : Classification de voitures#
Chargement des données#
Dans ce TP, nous voulons classifier des voitures, selon leur type (sportive, citadine, familiale…). Commençons par charger les données dans Basthon :
Télécharger les données (clic droit ici puis enregistrer la cible du lien sous).
Dans Basthon, cliquer sur Fichier puis Ouvrir et sélectionner le fichier téléchargé.
Exécuter le code ci-dessous, en modifiant titanic.csv si vous avez utilisé un autre nom de fichier.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
voitures = pd.read_csv("voitures.csv")
voitures
| nom | marque | cylindrée | chevaux | longueur | largeur | hauteur | poids | vitesse_max | 0_100 | consommation | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | panda | fiat | 1242 | 69 | 365 | 164 | 155 | 1030 | 164 | 15.0 | 5.7 |
| 1 | tt | audi | 2000 | 200 | 404 | 176 | 135 | 1400 | 235 | 7.0 | 7.0 |
| 2 | 208 | peugeot | 1200 | 100 | 398 | 174 | 146 | 1050 | 163 | 14.0 | 3.8 |
| 3 | c3 | citroën | 1124 | 61 | 385 | 167 | 152 | 998 | 157 | 16.0 | 5.4 |
| 4 | berlingo | citroën | 1360 | 75 | 411 | 172 | 180 | 1378 | 149 | 16.0 | 7.4 |
| 5 | clio 4 | renault | 1149 | 75 | 406 | 173 | 145 | 1105 | 177 | 12.0 | 5.0 |
| 6 | mégane 1 | renault | 1998 | 115 | 413 | 170 | 142 | 1085 | 197 | 9.7 | 7.3 |
| 7 | espace | renault | 1870 | 117 | 466 | 186 | 173 | 1897 | 176 | 14.0 | 9.7 |
| 8 | 2008 | peugeot | 1398 | 68 | 416 | 174 | 156 | 1200 | 190 | 9.5 | 5.7 |
| 9 | captur | renault | 1333 | 90 | 422 | 190 | 158 | 1352 | 180 | 10.0 | 6.5 |
| 10 | carrera gt | porsche | 5733 | 612 | 461 | 192 | 117 | 1385 | 330 | 4.0 | 18.0 |
| 11 | f40 | ferrari | 2936 | 478 | 443 | 198 | 113 | 1100 | 324 | 4.6 | 16.0 |
| 12 | scénic | renault | 1461 | 105 | 449 | 181 | 164 | 1700 | 190 | 11.0 | 7.0 |
Pour éviter d’utiliser des dataframe pandas, nous allons utiliser des listes attributs et noms tels que attributs[i] contienne les caractéristiques (cyindrée, chevaux, longueur…) et noms[i] le nom de la voiture \(i\) :
noms = voitures.iloc[:, :2].to_numpy().tolist()
noms[0] # affiche le nom de la première voiture
['panda', 'fiat']
attributs = voitures.iloc[:, 2:].to_numpy().tolist()
attributs[0] # affiche les valeurs des attributs de la première voiture
[1242.0, 69.0, 365.0, 164.0, 155.0, 1030.0, 164.0, 15.0, 5.7]
Pour obtenir la signification des attributs :
attributs_noms = voitures.columns[2:].to_numpy().tolist()
attributs_noms
['cylindrée',
'chevaux',
'longueur',
'largeur',
'hauteur',
'poids',
'vitesse_max',
'0_100',
'consommation']
Standardisation des données#
Question
Écrire une fonction moyenne(j) qui renvoie la moyenne de l’attribut j (c’est-à-dire la moyenne de attributs[i][j], pour tous les i possibles).
Solution
def moyenne(j):
return sum([x[j] for x in attributs])/len(attributs)
moyenne(7) # nombre moyen de secondes pour aller de 0 à 100 km/h
10.984615384615385
Question
Écrire une fonction ecart_type(j) qui renvoie l’écart-type de l’attribut j (c’est-à-dire \(\sigma = \sqrt{\sum_i \frac{(x_i - \mu)^2}{n}}\) où les \(x_i\) sont les valeurs pour l’attribut j et \(\mu\) est la moyenne de l’attribut j).
Solution
def ecart_type(j):
m = moyenne(j)
return (sum([(x[j] - m)**2 for x in attributs])/len(attributs))**0.5
ecart_type(0)
1206.7697505196386
Si des données \(x_1, ..., x_n\) ont une moyenne \(\mu\) et un écart-type \(\sigma\), on peut standardiser ces données, c’est-à-dire se ramener à une moyenne à \(0\) et un écart-type à \(1\), en remplaçant chaque \(x_i\) par :
Question
Définir une matrice X qui contient les caractéristiques standardisées des voitures.
Solution
X = []
for i in range(len(attributs)):
X.append([(attributs[i][j] - moyenne(j))/ecart_type(j) for j in range(len(attributs[i]))])
X[0]
[-0.5518865547576234,
-0.5838129204459943,
-1.881194060479367,
-1.4284117337371103,
0.3256520809467957,
-0.9620792816591849,
-0.6746501884297091,
1.034391681977312,
-0.5737524192504039]
Question
On aura aussi besoin de réaliser l’opération inverse de la précédente. Écrire une fonction inverse_standardisation(y) qui, pour une voiture y (c’est-à-dire la liste de ses attributs), renvoie une liste x telle que \(x_i = y_i \sigma_i + \mu_i\), où \(\mu_i\) et \(\sigma_i\) sont la moyenne et l’écart-type de l’attribut \(i\).
Solution
def inverse_standardisation(y):
return [y[i]*ecart_type(i) + moyenne(i) for i in range(len(y))]
inverse_standardisation(X[0]) # doit être égal à attributs[0]
[1242.0, 69.0, 365.0, 164.0, 155.0, 1030.0, 164.0, 15.0, 5.7]
Algorithme des k-moyennes#
Question
Écrire une fonction d(x, y) qui calcule la distance euclidienne entre deux attributs de voitures.
Solution
def d(x, y):
s = 0
for i in range(len(x)):
s += (x[i] - y[i])**2
return s**0.5
d(X[0], X[1])
3.6573045403567335
Question
Écrire une fonction centre(indices) qui renvoie le centre des X[i] pour i dans la liste indices.
Solution
def centre(indices):
c = [0]*len(X[0])
for i in indices:
for j in range(len(c)):
c[j] += X[i][j]
if len(indices) != 0:
for j in range(len(c)):
c[j] /= len(indices)
return c
centre([0, 2, 7]) # centre des voitures 0, 2 et 7
[-0.3900219295884706,
-0.42619570979982285,
-0.30720748345964605,
-0.35774636214316785,
0.48641703230027744,
0.16190614861559313,
-0.6103335371327435,
0.8626535994012577,
-0.4020041621721581]
Dans la suite, on utilisera une liste classes telle que classes[i] est la liste des indices j tels que X|j] est dans la classe i.
Par exemple, si classes = [[0, 8, 11], [2, 7]] alors la classe numéro \(0\) contient les voitures \(0\), \(8\), \(11\) (dont les valeurs sont X[0], X[8] et X[11]).
Question
Écrire une fonction calculer_centres(classes) qui renvoie une liste contenant les centres de chaque classe. Il faut donc que centres[i] soit le centre de la classe i.
Solution
def calculer_centres(classes):
centres = []
for c in classes:
centres.append(centre(c))
return centres
calculer_centres([[0, 8, 11], [2, 7]])
[[-0.04088048553760174,
0.2302101421317011,
-0.36593832588575514,
0.04375315220456059,
-0.4067215863301765,
-0.6579569555419957,
0.4128859153189823,
-0.3309260745023202,
0.2686318892762309],
[-0.30908961700389415,
-0.34738710447673715,
0.47978580505021445,
0.1775863236538034,
0.5667995079770183,
0.7238988637529822,
-0.5781752114842607,
0.7767845581132305,
-0.31613003363303516]]
On initialisera l’algorithme des k-moyennes avec des centres aléatoires en utilisant la fonction suivante :
def centres_aléatoires(k):
np.random.seed(1)
return np.random.rand(k, len(X[0])).tolist()
centres_aléatoires(2) # exemple de 2 centres aléatoires
[[0.417022004702574,
0.7203244934421581,
0.00011437481734488664,
0.30233257263183977,
0.14675589081711304,
0.0923385947687978,
0.1862602113776709,
0.34556072704304774,
0.39676747423066994],
[0.538816734003357,
0.4191945144032948,
0.6852195003967595,
0.20445224973151743,
0.8781174363909454,
0.027387593197926163,
0.6704675101784022,
0.41730480236712697,
0.5586898284457517]]
Question
Écrire une fonction plus_proche(i, centres) qui renvoie l’indice du centre le plus proche de la voiture X[i]. Il faut donc renvoyer j tel que d(X[i], centres[j]) est minimum.
Solution
def plus_proche(i, centres):
jmin = 0
for j in range(1, len(centres)):
d1 = d(X[i], centres[j])
if d1 < d(X[i], centres[jmin]):
jmin = j
return jmin
plus_proche(0, centres_aléatoires(4))
0
Question
Écrire une fonction calculer_classes(centres) qui renvoie une liste classes de même taille que centres et contenant les classes obtenues en associant chaque X[j] au centre le plus proche.
Ainsi, classes[i] doit contenir les indices j tel que le centre le plus proche de X[j] est centres[i].
Solution
def calculer_classes(centres):
classes = [[] for c in centres]
for i in range(len(X)):
classes[plus_proche(i, centres)].append(i)
return classes
calculer_classes(centres_aléatoires(3))
[[0, 1, 2, 3, 5, 6, 8, 9, 10, 11], [4], [7, 12]]
Question
Écrire une fonction k_moyennes(k) qui renvoie les classes obtenues par l’algorithme des k-moyennes appliqué aux données X.
Solution
def k_moyennes(k):
centres = centres_aléatoires(k)
while True:
classes = calculer_classes(centres)
centres2 = calculer_centres(classes)
if centres == centres2:
return classes, centres
centres = centres2
classes, centres = k_moyennes(3)
centres
[[2.010739827506566,
2.2652677985759393,
1.1845559141635222,
1.683209502457785,
-1.8178806037662938,
-0.15425435291040127,
2.1845173101353987,
-1.7220045433683606,
2.198755159298423],
[-0.39288770686855584,
-0.42594631547918027,
-0.6566559958949947,
-0.7006938639818525,
0.13139443139467197,
-0.4840370002937282,
-0.41153661494212246,
0.36461315993070004,
-0.5216145554945079],
[-0.29279266668822856,
-0.3743216911061462,
0.9613787129443082,
0.7463773023130854,
0.861535252125068,
1.393601569390209,
-0.3589139002446052,
0.1757012690970402,
-0.07486462488026106]]
Question
Écrire une fonction inertie(classes, centres) qui renvoie la somme des carrés des distances des voitures aux centres de leurs classes.
Solution
def inertie(classes, centres):
s = 0
for i in range(len(classes)):
for j in classes[i]:
s += d(X[j], centres[i])**2
return s
Question
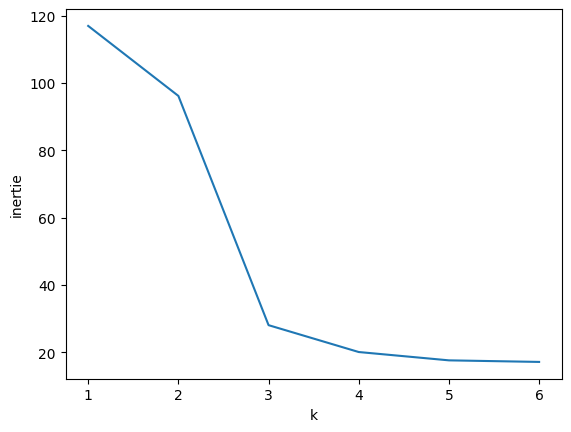
Exécuter le code suivant pour afficher l’inertie en fonction du nombre de classes \(k\). Quel \(k\) vous semble optimal ?
kmax = 6
I = []
for k in range(1, kmax+1):
classes,centres = k_moyennes(k)
I.append(inertie(classes, centres))
plt.plot(range(1, kmax+1), I)
plt.xlabel("k")
plt.ylabel("inertie")
plt.show()
Question
On prend la valeur de \(k\) obtenue à la question précédente. Pour chaque classe, afficher les voitures de cette classe ainsi que le centre (en appliquant inverse_standardisation dessus).
Solution
classes, centres = k_moyennes(4)
for i in range(len(centres)):
print("Centre", i, ":", inverse_standardisation(centres[i]))
for j in classes[i]:
print(" ", noms[j])
print()
Question
Pour savoir ce qui différencie deux classes, on peut regarder les coordonnées du vecteur dont les extrémités sont les centres des deux classes. Quelles sont les caractéristiques qui différencient les voitures familiale des voitures citadines ? Les voitures sportives des voitures citadines ?
Solution
attributs_noms
['cylindrée',
'chevaux',
'longueur',
'largeur',
'hauteur',
'poids',
'vitesse_max',
'0_100',
'consommation']
Solution
np.array(centres[1]) - np.array(centres[3])
array([-0.31896446, -0.1361693 , -1.88526004, -1.02047793, -1.22359991,
-2.32875335, -0.11255414, 0.15027082, -0.75037631])


