TP 1 : Programmation dynamique#

Coefficient binomial#

On souhaite calculer $\binom{n}{k}$ par programmation dynamique, en utilisant la formule de Pascal :

\[\binom{n}{k} = \binom{n - 1}{k - 1} + \binom{n - 1}{k}\]

Question

Que peut-on prendre comme cas de base ?

Solution

\[\binom{0}{k} = 0\]

\[\binom{n}{0} = 1, \text{si } n \neq 0\]

Question

Écrire une fonction récursive binom_rec(n, k) renvoyant $\binom{n}{k}$ à partir de la formule ci-dessus. Expliquer pourquoi la complexité de cette fonction est très mauvaise.

Solution

def binom_rec(n, k): # voir cours
    if k == 0:
        return 1
    if n == 0:
        return 0
    return binom_rec(n - 1, k - 1) + binom_rec(n - 1, k)

binom_rec(20, 4)

Question

Écrire une fonction binom_dp(n, k) renvoyant $\binom{n}{k}$ en utilisant la même formule, mais par programmation dynamique.
Pour cela, on pourra stocker $\binom{n}{k}$ dans une matrice (ou : un dictionnaire) et la remplir par $n$ croissant et par $k$ croissant.

def binom_dp(n, k):
    # définir une matrice M de taille (n+1)x(k+1)
    # M[i][j] contiendra j parmi i
    for i in range(0, n + 1):
        M[i][0] = ... # cas de base
        for j in range(1, k + 1):
            M[i][j] = ... # récurrence
    return ...

Solution

def binom_dp(n, k):
    M = [[0]*(k + 1) for _ in range(n + 1)]
    for i in range(0, n + 1):
        M[i][0] = 1 # cas de base

    for i in range(1, n + 1):
        for j in range(1, k + 1):
            M[i][j] = M[i - 1][j - 1] + M[i - 1][j]
    return M[n][k]

binom_dp(20, 4)

Question

Écrire une fonction binom_memo(n, k) renvoyant $\binom{n}{k}$ en utilisant le même principe, mais avec mémoïsation plutôt que programmation dynamique.

def binom_memo(n, k):
    d = {} # d[(i, j)] contiendra j parmi i
    def aux(i, j): # renvoie j parmi i
        ... # cas de base
        ... # dans le cas général, regarder si (i, j) est dans d : si oui, renvoyer la valeur associée, sinon la calculer et l'ajouter à d
    return aux(n, k)

Solution

def binom(n, k):
    d = {}
    def aux(i, j):
        if j == 0: return 1
        if i == 0: return 0
        if (i, j) not in d:
            d[(i, j)] = aux(i - 1, j - 1) + aux(i - 1, j)
        return d[(i, j)]
    return aux(n, k)

Rendu de monnaie#

Étant donnée une liste L d’entiers $a_1,\ldots,a_k$ (des pièces), on veut calculer le nombre minimum $r(n, k)$ de pièces parmi $a_1, ..., a_k$ dont la somme vaut $n$.

Par exemple, si $k = 3$ et $a_1 = 1, a_2 = 2, a_3 = 5$ alors $r(7, 3) = 2$ (car $7 = 2 + 5$ et c’est la façon de rendre $7$€ qui utilise le moins de pièces).

Remarques :

On peut utiliser plusieurs fois la même pièce.
$r(0, k)$ revient à rendre $0$€, ce qu’on peut faire avec $0$ pièce : $r(0, k) = 0$
$r(n, 0)$ revient à n’utiliser aucune pièce, ce qui est impossible si $n \neq 0$ : on posera $r(n, 0)$ = $\infty$ (float("inf") en Python).

Question

Écrire une relation de récurrence sur $r(n, k)$. On pourra distinguer deux cas pour rendre $n$ euros avec les picèes $a_1$, …, $a_k$ :

soit $a_k$ n’est pas utilisée (et on a donc $r(n, k) = r(n, k - 1)$)
soit $a_k$ est utilisée (et on a $r(n, k) = ...$).

Comme on ne sait pas si $a_k$ est utilisée ou non, on a dans le cas général : $r(n, k) = \min(..., ...)$.

Solution

Si $a_k$ est utilisée : il faut encore rendre $n - a_k$ euros avec les pièces $a_1$, …, $a_k$ (on a le droit d’utiliser plusieurs fois $a_k$), d’où $r(n, k) = r(n - a_k, k) + 1$.

Dans le cas général, on considère les deux possibilités et on conserve le minimum : $$ r(n, k) = min(r(n, k - 1), r(n - a_k, k) + 1) $$

Remarque : on ne peut utiliser $a_k$ pour rendre $n$ euros que si $n \geq a_k$. Si $n < a_k$, on a donc $r(n, k) = r(n, k - 1)$.

Question

En déduire une fonction rendu(L, n) par programmation dynamique renvoyant le nombre minimum de pièces requises pour rendre n euros, où L est la liste des pièces.
On remplira une matrice M pour que M[i][j] contienne le nombre minimum de pièces pour rendre i euros en utilisant les j premières pièces de L.

Solution

def rendu(L, n):
    k = len(L) # nombre de pièces
    M = [[0]*(k + 1) for _ in range(n + 1)]
    for i in range(1, n + 1):
        M[i][0] = float("inf")
        for j in range(1, k + 1):
            if i - L[j - 1] >= 0:
                M[i][j] = min(M[i][j - 1], 1 + M[i - L[j - 1]][j])
            else:
                M[i][j] = M[i][j - 1]
    return M[-1][-1]

rendu([1, 2, 5], 7)

Question

Réécrire la fonction précédente par mémoïsation plutôt que par programmation dynamique.

Solution

def rendu_memo(L, n):
    k = len(L)
    d = {}
    def aux(i, j):
        if (i, j) in d:
            return d[(i, j)]
        if i == 0:
            return 0
        if j == 0:
            return float("inf")
        if i - L[j - 1] >= 0:
            d[(i, j)] = min(aux(i, j - 1), 1 + aux(i - L[j - 1], j))
        else:
            d[(i, j)] = aux(i, j - 1)
        return d[(i, j)]
    return aux(n, k)
rendu_memo([1, 2, 5], 7)

Plus grand carré dans une matrice#

Étant donnée une matrice carrée remplie de 0 ou 1, on souhaite connaître la taille du plus gros carré de 1 dans cette matrice.
Par exemple, ce nombre est 2 pour la matrice $M$ suivante (correspondant au carré en pointillé) :

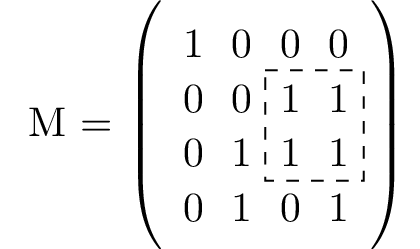
La case de coordonnés $(x, y)$ est celle sur la ligne $x$, colonne $y$. La case de coordonnées (0, 0) est celle en haut à gauche.
On supposera que les indices en arguments des fonctions ne dépassent pas des tableaux ou matrices correspondants.

Question

Définir M en Python.

Solution

M = [[1, 0, 0, 0], [0, 0, 1, 1], [0, 1, 1, 1], [0, 1, 0, 1]]

Méthode naïve#

Question

Écrire une fonction est_carre telle que est_carre(m, x, y, k) détermine si la sous-matrice de m de taille $k \times k$ et dont la case en haut à gauche a pour coordonnées (x, y) ne possède que des 1.

Solution

def est_carre(M, x, y, k):
    for i in range(x, x + k):
        for j in range(y, y + k):
            if M[i][j] != 1:
                return False
    return True

assert(est_carre(M, 1, 2, 2) and not est_carre(M, 1, 1, 2))

Question

Écrire une fonction contient_carre telle que contient_carre(m, k) renvoie true si m contient un carré de 1 de taille $k$, false sinon.

Solution

def contient_carre(M, k):
    n = len(M)
    for i in range(n - k + 1):
        for j in range(n - k + 1):
            if est_carre(M, i, j, k):
                return True
    return False

assert(contient_carre(M, 2) and not contient_carre(M, 3))

Question

Écrire une fonction max_carre1 telle que max_carre1(m) renvoie la taille maximum d’un carré de 1 contenu dans m.

Solution

def max_carre1(M):
    n = len(M)
    for k in range(n, 0, -1):
        if contient_carre(M, k):
            return k
    return 0

max_carre1(M)

Question

Quelle est la complexité de max_carre1(m) dans le pire cas ?

Solution

est_carre(M, x, y, k) est en $O(k^2)$.
contient_carre(M, k) appelle O($n$) fois est_carre, donc est en $O(n^2 k^2)$.
max_carre1(M) appelle contient_carre pour $k = 1, 2, ..., n$, donc est de complexité $\sum_{k=1}^n O(n^2 k^2) = O(n^3 \sum_{k=1}^n k^2)$. Comme $\sum_{k=1}^n k^2 = \frac{n(n+1)(2n+1)}{6} = O(n^3)$, la complexité totale est $\boxed{O(n^6)}$.`

On va construire une matrice c telle que c[x][y] est la taille maximum d’un carré de 1 dans m dont la case en bas à droite est m[x][y] (c’est à dire un carré de 1 qui contient m[x][y] mais aucun m[i][j] si $i > x$ ou $j > y$).
Par exemple, c[1][2] = 1 et c[2][3] = 2 pour la matrice $M$ ci-dessus.

Question

Que vaut c[0][y] et c[x][0] ?

Solution

c[0][y] = 0 si m[0][y] = 0 et c[0][y] = 1 sinon.
De même pour c[x][0].
Remarque : c[0][y] et c[x][0] sont donc les mêmes valeurs que m[0][y] et m[x][0], on peut donc initialiser c comme une copie de m.

Question

Que vaut c[x][y] si m[x][y] = 0 ?

Solution

c[x][y] = 0.

Question

Montrer que, si m[x][y] = 1, c[x][y] = 1 + min(c[x-1][y], c[x][y-1], c[x-1][y-1]).

Question

En déduire une fonction max_carre2 telle que max_carre2(m) renvoie la taille maximum d’un carré de 1 contenu dans m, ainsi que les coordonnées de la case en haut à gauche d’un tel carré.

Solution

def max_carre2(m):
    c = m.copy()
    for i in range(len(m)):
        for j in range(len(m[0])):
            if m[i][j] == 1:
                c[i][j] = 1 + min(c[i - 1][j], c[i][j - 1], c[i - 1][j - 1])
    return max(max(l) for l in c)

max_carre2(M)

Question

Quelle est la complexité de max_carre2(m), en fonction des dimensions de m? Comparer avec max_carre1(m).

Solution

max_carre2(m) est en $\boxed{O(n^2)}$ à cause des deux boucles for imbriquées.
C’est donc beaucoup mieux que max_carre1(m) qui est en $O(n^6)$.

Pour ceux qui ont fini#

Cette partie n’est pas à rendre, sauf si vous en avez le temps.

Question

S’inscrire sur https://projecteuler.net/ et résoudre ce problème.
On pourra télécharger le fichier triangle.txt demandé avec :

import urllib.request
f = urllib.request.urlopen("https://projecteuler.net/project/resources/p067_triangle.txt")
lignes = list(map(lambda x : list(map(int, x.split())), f.readlines())) # renvoie la liste des lignes du fichier

Question

Résoudre ce problème (en s’inscrivant préalablement)

Informatique commune en 2ème année de CPGE

TP 1 : Programmation dynamique

Contents

TP 1 : Programmation dynamique#

Coefficient binomial#

Rendu de monnaie#

Plus grand carré dans une matrice#

Méthode naïve#

Pour ceux qui ont fini#