TP : Jeu du domineering
TP : Jeu du domineering#
Le domineering est un jeu de plateau où le joueur 0 place un domino vertical et le joueur 1 un domino horizontal. Un joueur qui ne peut plus jouer perd.
Voici un exemple de partie (de gauche à droite) où le joueur 1 gagne :

Une configuration est représentée par une matrice (-1 = vide, 0 = joueur 0, 1 = joueur 1)
Question
Écrire une fonction grille_vide(n, p) qui renvoie une grille de taille \(n \times p\) vide (remplie de \(-1\)).
Solution
def grille_vide(n, p):
return [[-1 for j in range(p)] for i in range(n)]
grille_vide(3, 4)
[[-1, -1, -1, -1], [-1, -1, -1, -1], [-1, -1, -1, -1]]
Question
Écrire une fonction coups_possibles(v, joueur) qui prend en entrée une configuration v et qui renvoie la liste des positions \((i, j)\) où le joueur joueur peut placer son domino (le joueur \(0\) place un domino en position \((i, j)\) et \((i+1, j)\) et le joueur \(1\) en position \((i, j)\) et \((i, j+1)\)).
Solution
def coups_possibles(v, joueur):
coups = []
for i in range(len(v)):
for j in range(len(v[0])):
if joueur == 0 and i < len(v) - 1 and v[i][j] == v[i + 1][j] == -1:
coups.append((i, j))
if joueur == 1 and j < len(v[0]) - 1 and v[i][j] == v[i][j + 1] == -1:
coups.append((i, j))
return coups
print(coups_possibles(grille_vide(3, 4), 0))
print(coups_possibles(grille_vide(3, 4), 1))
[(0, 0), (0, 1), (0, 2), (0, 3), (1, 0), (1, 1), (1, 2), (1, 3)]
[(0, 0), (0, 1), (0, 2), (1, 0), (1, 1), (1, 2), (2, 0), (2, 1), (2, 2)]
Question
Écrire une fonction strategie_aleatoire(v, joueur) qui prend en entrée une configuration v et qui renvoie un coup choisi au hasard parmi les coups possibles.
On pourra utiliser la fonction random.choice(L) qui renvoie un élément au hasard dans L (en n’oubliant pas import random).
Solution
import random
def strategie_aleatoire(v, joueur):
coups = coups_possibles(v, joueur)
return random.choice(coups)
strategie_aleatoire(grille_vide(3, 4), 0) # coup aléatoire
(0, 3)
Question
Écrire une fonction placer(v, i, j, joueur) qui prend en entrée une configuration v, une position \((i, j)\) et un joueur joueur et qui modifie v en plaçant le domino du joueur joueur à la position \((i, j)\).
Plus précisément, si joueur == 0, alors on place un domino sur les cases \((i, j)\) et \((i + 1, j)\), et si joueur == 1, alors on place un domino sur les cases \((i, j)\) et \((i, j + 1)\).
Solution
def placer(v, i, j, joueur):
v[i][j] = joueur
if joueur == 0:
v[i + 1][j] = joueur
else:
v[i][j + 1] = joueur
Question
Écrire une fonction retirer(v, i, j, joueur) qui prend en entrée une configuration v, une position \((i, j)\) et un joueur joueur et qui modifie v en retirant le domino du joueur joueur à la position \((i, j)\).
Solution
def retirer(v, i, j, joueur):
v[i][j] = -1
if joueur == 0:
v[i + 1][j] = -1
else:
v[i][j + 1] = -1
Question
Écrire une fonction jeu(strategie0, strategie1, n, p) qui prend en entrée deux stratégies et qui renvoie le joueur qui gagne.
strategie0(v, 0) renvoie un couple \((i, j)\) correspondant au coup du joueur 0, et strategie1(v, 1) renvoie le coup du joueur 1.
Il faut donc partir d’une grille de taille \(n\times p\) et faire jouer les joueurs chacun son tour avec leur stratégie, jusqu’à ce qu’un joueur ne puisse plus jouer (qui est donc le perdant).
Solution
def jeu(strategie0, strategie1, n, p):
v = grille_vide(n, p)
joueur = 0
while coups_possibles(v, joueur) != []:
if joueur == 0:
i, j = strategie0(v, 0)
else:
i, j = strategie1(v, 1)
placer(v, i, j, joueur)
joueur = 1 - joueur
return 1 - joueur
jeu(strategie_aleatoire, strategie_aleatoire, 3, 4) # 0 ou 1
0
Question
Écrire une fonction statistiques(strategie0, strategie1, n, p, nb_parties) qui prend en entrée deux stratégies, qui appelle nb_parties fois la fonction jeu et qui renvoie le nombre de parties gagnées par chaque joueur.
Tester avec différentes tailles initiales de la grille.
Solution
def statistiques(strategie1, strategie2, n, p, nb_parties):
victoires = [0, 0]
for i in range(nb_parties):
gagnant = jeu(strategie1, strategie2, n, p)
victoires[gagnant] += 1
return victoires
statistiques(strategie_aleatoire, strategie_aleatoire, 3, 10, 1000)
[388, 612]
Question
Écrire une fonction h1(v) renvoyant la différence entre le nombre de cases libres pour le joueur 0 et le nombre de cases libres pour le joueur 1. On renverra \(\infty\) (float('inf')) si le joueur 0 a gagné et \(-\infty\) (float('-inf')) si le joueur 1 a gagné.
Solution
def h1(v):
if len(coups_possibles(v, 0)) == 0:
return -float('inf')
if len(coups_possibles(v, 1)) == 0:
return float('inf')
return len(coups_possibles(v, 0)) - len(coups_possibles(v, 1))
h1(grille_vide(3, 2))
1
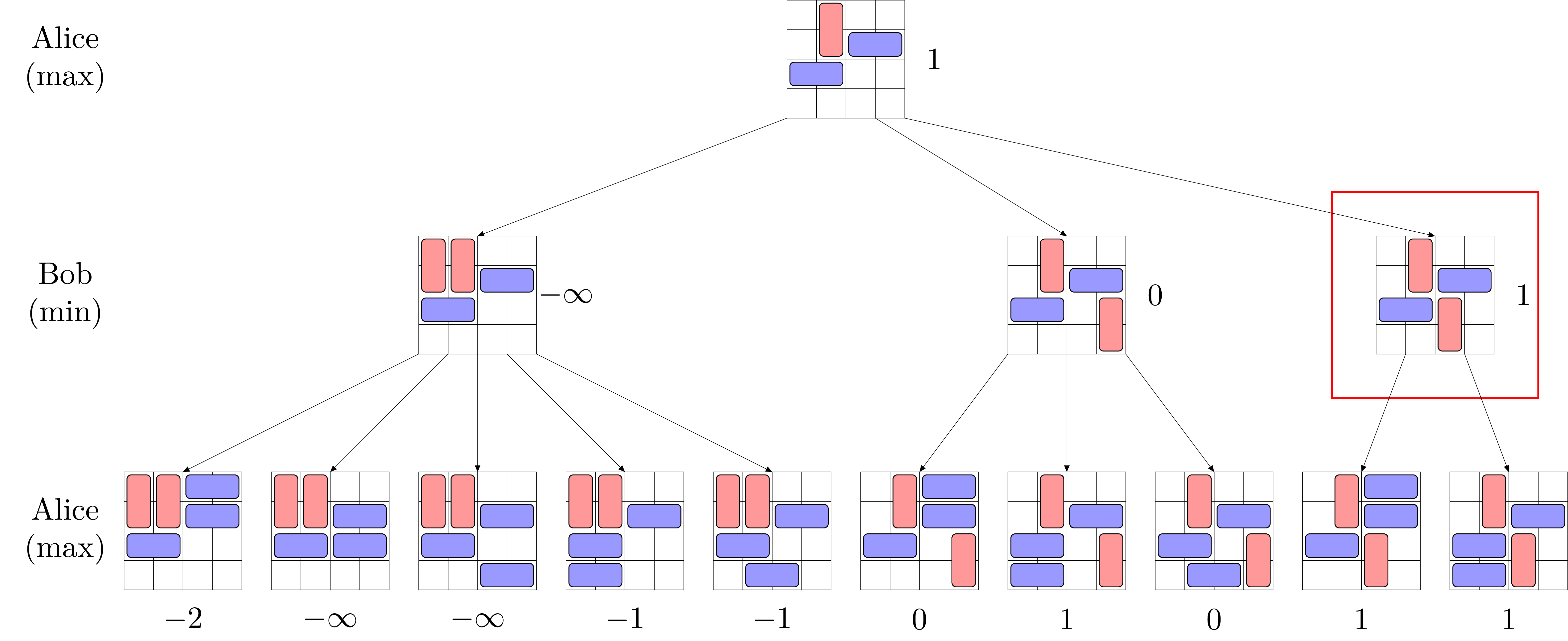
L’algorithme min-max considère, depuis la position en cours, toutes les positions atteignables après \(p\) coups et conserver celle ayant la meilleure heuristique.
Puis on donne récursivement une valeur à chaque sommet v de l’arbre :
si
vest à profondeur \(0\), on renvoie l’heuristique devsinon, si le joueur \(0\) doit jouer, on renvoie la valeur maximum des successeurs de
v(le joueur \(0\) veut maximiser sa valeur)sinon, si le joueur \(1\) doit jouer, on renvoie la valeur minimum des successeurs de
v(le joueur \(1\) veut minimiser la valeur de son adversaire)
On choisit le coup qui donne la meilleure valeur parmi les coups possibles.
Question
Écrire une fonction minmax(v, joueur, profondeur, h) qui prend en entrée une configuration v, un joueur joueur, une profondeur profondeur et une fonction heuristique h et qui renvoie un couple (valeur, coup) où coup est le meilleur coup à jouer et valeur est sa valeur.
def minmax(v, joueur, profondeur, h): # renvoie (valeur, coup)
coups = coups_possibles(v, joueur)
# si la profondeur est 0 ou s'il n'y a pas de coup possible, renvoyer (h(v), None)
else:
if joueur == 0:
# stocker la meilleure valeur et le meilleur coup dans des variables
for coup in coups:
# jouer un coup (avec la fonction placer)
# appel récursif pour obtenir la valeur du coup
# retirer le coup
# si la valeur du coup est meilleure que la meilleure valeur, mettre à jour la meilleure valeur et le meilleur coup
# renvoyer la meilleure valeur et le meilleur coup
else:
# de même pour le joueur 1
Solution
def minmax(v, joueur, profondeur, h):
coups = coups_possibles(v, joueur)
if coups == [] or profondeur == 0:
return h(v), None
else:
if joueur == 0:
meilleur_coup = coups[0]
meilleur_score = -float('inf')
for coup in coups:
placer(v, coup[0], coup[1], joueur)
score, _ = minmax(v, 1 - joueur, profondeur - 1, h)
retirer(v, coup[0], coup[1], joueur)
if score > meilleur_score:
meilleur_score = score
meilleur_coup = coup
return meilleur_score, meilleur_coup
else:
meilleur_coup = coups[0]
meilleur_score = float('inf')
for coup in coups:
placer(v, coup[0], coup[1], joueur)
score, _ = minmax(v, 1 - joueur, profondeur - 1, h)
retirer(v, coup[0], coup[1], joueur)
if score < meilleur_score:
meilleur_score = score
meilleur_coup = coup
return meilleur_score, meilleur_coup
Question
En déduire une fonction strategie_minmax(v, joueur) qui prend en entrée une configuration v et un joueur joueur et qui renvoie le meilleur coup à jouer selon l’algorithme min-max avec l’heuristique h1 et, par exemple, une profondeur de 2.
Tester avec la fonction ci-dessous pour vérifier que la stratégie min-max est meilleure que la stratégie aléatoire.
Solution
def strategie_minmax(v, joueur):
_, coup = minmax(v, joueur, 2, h1)
return coup
statistiques(strategie_minmax, strategie_aleatoire, 5, 5, 10)
[10, 0]


